题目内容
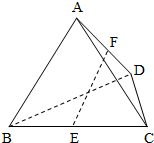 在正四面体A-BCD中,E、F分别是BC、AD的中点.
在正四面体A-BCD中,E、F分别是BC、AD的中点.(1)求异面直线AB与DE所成角的余弦值;
(2)求异面直线BF与DE所成角的余弦值;
(3)求异面直线AB与CD所成角的大小.
考点:异面直线及其所成的角
专题:空间位置关系与距离,空间角
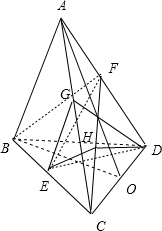
分析:(1)设正四面体的棱长为1,取AC中点G,连结EG,DG,得∠EGD是异面直线AB与DE所成角(或所成角的补角),由此能求出异面直线AB与DE所成角的余弦值.
(2)连结CF,取CF中点H,连结EH,DH,得∠EHD是异面直线BF与DE所成角(或所成角的补角),由此能求出异面直线BF与DE所成角的余弦值.
(3)取CD中点O,连结AO,BO,推导出CD⊥平面ABO,由此能求出异面直线AB与CD所成角的大小.
(2)连结CF,取CF中点H,连结EH,DH,得∠EHD是异面直线BF与DE所成角(或所成角的补角),由此能求出异面直线BF与DE所成角的余弦值.
(3)取CD中点O,连结AO,BO,推导出CD⊥平面ABO,由此能求出异面直线AB与CD所成角的大小.
解答:
解:(1)设正四面体的棱长为1,
取AC中点G,连结EG,DG,
∵E是BC中点,G是AC中点,∴EG∥AB,
∴∠EGD是异面直线AB与DE所成角(或所成角的补角),
∵DE=DG=
=
,EG=
AB=
,
∴cos∠DGE=
=
.
∴异面直线AB与DE所成角的余弦值为
.
(2)连结CF,取CF中点H,连结EH,DH,
∵E是BC中点,H是CF中点,∴EH∥BF,
∴∠EHD是异面直线BF与DE所成角(或所成角的补角),
∵DE=
,EH=
BF=
,DH=
=
,
∴cos∠EHD=
=-
,
∴异面直线BF与DE所成角的余弦值为
.
(3)取CD中点O,连结AO,BO,
∵AD=AC,BD=BC,∴AO⊥CD,BO⊥CD,
∴CD⊥平面ABO,∴CD⊥AB,
∴异面直线AB与CD所成角的大小为90°.
取AC中点G,连结EG,DG,
∵E是BC中点,G是AC中点,∴EG∥AB,
∴∠EGD是异面直线AB与DE所成角(或所成角的补角),
∵DE=DG=
1-
|
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴cos∠DGE=
(
| ||||||||||
2×
|
| ||
| 6 |

∴异面直线AB与DE所成角的余弦值为
| ||
| 6 |
(2)连结CF,取CF中点H,连结EH,DH,
∵E是BC中点,H是CF中点,∴EH∥BF,
∴∠EHD是异面直线BF与DE所成角(或所成角的补角),
∵DE=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
|
| ||
| 4 |
∴cos∠EHD=
| ||||||||
2×
|
| ||
| 21 |
∴异面直线BF与DE所成角的余弦值为
| ||
| 21 |
(3)取CD中点O,连结AO,BO,
∵AD=AC,BD=BC,∴AO⊥CD,BO⊥CD,
∴CD⊥平面ABO,∴CD⊥AB,
∴异面直线AB与CD所成角的大小为90°.
点评:本题考查直线与平面所成角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
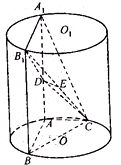 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.