题目内容
已知函数f(x)=|x-1|+|x+1|,不等式f(x)≥4的解集为M.
(Ⅰ)求M;
(Ⅱ)当a,b∈M时,证明:|
+
|≥|
+1|.
(Ⅰ)求M;
(Ⅱ)当a,b∈M时,证明:|
| a |
| 2 |
| 2 |
| b |
| a |
| b |
考点:绝对值不等式的解法
专题:
分析:(Ⅰ)由题意可得 f(x)=
,分类讨论求得不等式f(x)≥4的解集M.
(Ⅱ)由题意可得a2≥4,b2≥4,计算左边的平方减去右边的平方的结果大于或等于零,不等式得证.
|
(Ⅱ)由题意可得a2≥4,b2≥4,计算左边的平方减去右边的平方的结果大于或等于零,不等式得证.
解答:
解:(Ⅰ)由题意可得 f(x)=|x-1|+|x+1|=
,
当x<-1时,由-2x≥4,得x≤-2;
当-1≤x≤1时,由f(x)=2<4可得不等式f(x)≥4无解;
当x>1时,由2x≥4,得x≥2;
所以M={x|x≤-2,或x≥2}.
(Ⅱ)当a,b∈M时,即a2≥4,b2≥4,
∵(
+
)2-(
+1)2=
+
-
-1=
≥0,
∴(
+
)2≥(
+1)2,∴|
+
|≥|
+1|.
|
当x<-1时,由-2x≥4,得x≤-2;
当-1≤x≤1时,由f(x)=2<4可得不等式f(x)≥4无解;
当x>1时,由2x≥4,得x≥2;
所以M={x|x≤-2,或x≥2}.
(Ⅱ)当a,b∈M时,即a2≥4,b2≥4,
∵(
| a |
| 2 |
| 2 |
| b |
| a |
| b |
| a2 |
| 4 |
| 4 |
| b2 |
| a2 |
| b2 |
| (a2-4)(b2-4) |
| 4b2 |
∴(
| a |
| 2 |
| 2 |
| b |
| a |
| b |
| a |
| 2 |
| 2 |
| b |
| a |
| b |
点评:本题主要考查绝对值不等式的解法,体现了等价转化和分类讨论的数学思想,用比较法证明不等式,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
正方体ABCD-A1B1C1D1中,异面直线B1D1与DC1所成角的大小是( )
| A、30° | B、60° |
| C、45° | D、90° |
平面向量
与
的夹角为60°,
=(1,0),|
|=1,则
•(
-3
)等于( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
| D、1 |
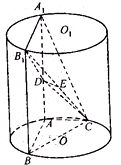 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.