题目内容
设f(x)=lnx+ax(a∈R且a≠0).
(1)讨论函数f(x)的单调性;
(2)若a=1,证明:x∈[1,2]时,f(x)-3<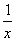 成立.
成立.
(1)函数f(x)的定义域为(0,+∞),f ′(x)=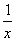 +a,
+a,
当a>0时,f ′(x)>0,∴函数f(x)在(0,+∞)上是增函数.
当a<0时,f ′(x)=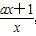 ,
,
由f ′(x)>0得0<x<-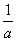 ;由f ′(x)<0得,x>-
;由f ′(x)<0得,x>-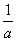 .
.
∴函数f(x)在(0,-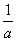 )上是增函数;在(-
)上是增函数;在(-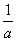 ,+∞)上是减函数.
,+∞)上是减函数.
(2)当a=1时,f(x)=lnx+x,
要证x∈[1,2]时,f(x)-3<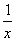 成立,
成立,
只需证xlnx+x2-3x-1<0在x∈[1,2]时恒成立.
令g(x)=xlnx+x2-3x-1,则g′(x)=lnx+2x-2,
设h(x)=lnx+2x-2,则h′(x)=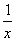 +2>0,
+2>0,
∴h(x)在[1,2]上单调递增,∴g′(1)≤g′(x)≤g′(2),即0≤g′(x)≤ln2+2,
∴g(x)在[1,2]上单调递增,∴g(x)≤g(2)=2ln2-3<0,∴当x∈[1,2]时,xlnx+x2-3x-1<0恒成立,即原命题得证.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目

 D.
D.
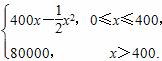 则总利润最大时,每年生产的产品产量是( )
则总利润最大时,每年生产的产品产量是( ) (0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和. =(1,-2),
=(1,-2), =(a,-1),
=(a,-1), =(-b,0),且A,B,C三点共线,则
=(-b,0),且A,B,C三点共线,则 的最小值为________.
的最小值为________.