题目内容
sin165°= ．
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：由条件利用诱导公式进行化简求值，可得结果．
解答：
解：sin165°=sin（180°-15°）=sin15°=sin（45°-30°）
=sin45°cos30°-cos45°sin30°=
×
-
×
=
，
故答案为：
．
=sin45°cos30°-cos45°sin30°=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||||
| 4 |
故答案为：
| ||||
| 4 |
点评：本题主要考查利用诱导公式进行化简求值，属于基础题．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
下列命题中，正确的是（ ）
| A、底面是正方形的四棱柱是正方体 |
| B、棱锥的高线不可能在几何体之外 |
| C、过棱锥顶点的一个平面把棱锥分成两部分，每一部分形成的几何体仍然是棱锥 |
| D、在所有棱柱中，互相平行的面最多有三对 |
复数 z=x+yi（x，y∈R）满足方程|z-1|=2|z|，则在复平面上表示复数z的动点Z的轨迹图形是（ ）
| A、直线 | B、圆 | C、椭圆 | D、抛物线 |
y=|sinx|+|cosx|的最小正周期为（ ）
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
已知角α的终边上一点的坐标为（sin
，cos
），则角α的最小正值为（ ）
| π |
| 3 |
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
D、E、F分别是△ABC三边BC、CA、AB中点，则
+
+
=（ ）
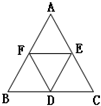
| DE |
| EF |
| DF |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
经过点（-1，1），倾斜角是直线y=
x-2的倾斜角的2倍的直线方程是（ ）
| ||
| 2 |
| A、x=-1 | ||
| B、y=1 | ||
C、y-1=
| ||
D、y-1=2
|