题目内容
计算：（
-tan
）•（1+tanα•tan
）= ．
| 1 | ||
tan
|
| α |
| 2 |
| α |
| 2 |
考点：二倍角的正切
专题：三角函数的求值
分析：直接利用二倍角公式以及切化弦化简求解即可．
解答：
解：（
-tan
）•（1+tanα•tan
）
=
•（1+tanα•tan
）
=
+2tan
=
+
=
+
=
．
故答案为：
．
| 1 | ||
tan
|
| α |
| 2 |
| α |
| 2 |
=
cos2
| ||||
sin
|
| α |
| 2 |
=
| 2cosα |
| sinα |
| α |
| 2 |
=
| 2cosα |
| sinα |
2sin2
| ||||
cos
|
=
| 2cosα |
| sinα |
| -2cosα+2 |
| sinα |
=
| 2 |
| sinα |
故答案为：
| 2 |
| sinα |
点评：本题考查弦切互化，二倍角公式的应用，考查计算能力．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
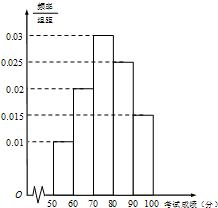某市为了了解本市高中学生的汉字书写水平，在全市范围内随机抽取了近千名学生参加汉字听写考试，将所得数据整理后，绘制出频率分布直方图如图所示，其中样本数据分组区间为[50，60），[60，70），[70，80），[80，90），[90，100]．