题目内容
一个等比数列{an}共有2n+1项，其奇数项之积为100，偶数项之积为120，求an+1．
考点：等比数列的性质
专题：等差数列与等比数列
分析：根据等比数列的通项公式和性质，利用整体法即可得到结论．
解答：
解：∵等比数列{an}共有2n+1项，且奇数项之积为100，偶数项之积为120，
∴T奇=a1a3???a2n+1=100，T偶=a2a4???a2n=120，
∴
=
=a1(
)???(
)=a1qn=an+1，
即an+1=
=
．
∴T奇=a1a3???a2n+1=100，T偶=a2a4???a2n=120，
∴
| T奇 |
| T偶 |
| a1a3???a2n+1 |
| a2a4???a2n |
| a3 |
| a2 |
| a2n+1 |
| a2n |
即an+1=
| 100 |
| 120 |
| 5 |
| 6 |
点评：本题主要考查等比数列的性质和通项公式的应用，要求熟练掌握等比数列的性质的应用，考查学生计算能力．
练习册系列答案
阅读快车系列答案
相关题目
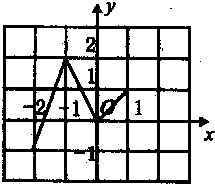已知定义在R上的函数f（x）满足f（x）=f（x+3），如图表示 该函数在区间（-2，1]上的图象，则f（2011）+f（2012）等于（ ）
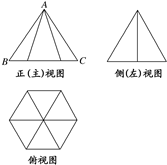一个几何体的三视图如图所示，其中正（主）视图中△ABC是边长为2的正三角形，俯视图的边界为正六边形，那么该几何体的侧）视图的面积为（ ）