题目内容
已知函数f(x)=2sin(2x+
)+1,
(Ⅰ)用“五点法”画出该函数在一个周期内的简图;
(Ⅱ)写出该函数的单调递减区间.
| π |
| 3 |
(Ⅰ)用“五点法”画出该函数在一个周期内的简图;
(Ⅱ)写出该函数的单调递减区间.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:计算题,三角函数的图像与性质
分析:(Ⅰ)令2x+
=0,
,π,
,2π,得到相应的x的值与y的值,列表,描点即可;
(Ⅱ)由图,可求得该函数的单调递减区间.
| π |
| 3 |
| π |
| 2 |
| 3π |
| 2 |
(Ⅱ)由图,可求得该函数的单调递减区间.
解答:
解:(Ⅰ)列表,描点,连线
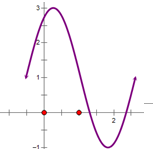
(Ⅱ)由2kπ+
≤2x+
≤2kπ+
(k∈Z)得:kπ+
≤x≤kπ+
(k∈Z),
∴函数f(x)=2sin(2x+
)+1的单调递减区间:为[
+kπ,
+kπ](k∈Z).
2x+
|
0 |
|
π |
|
2π | ||||||||||
| x | -
|
|
|
|
| ||||||||||
| y | 1 | 3 | 1 | -1 | 1 |

(Ⅱ)由2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
∴函数f(x)=2sin(2x+
| π |
| 3 |
| π |
| 12 |
| 7π |
| 12 |
点评:本题考查“五点法”作函数在一个周期内的简图,考查正弦函数的单调区间的确定,考查运算能力,属于中档题.

练习册系列答案
相关题目
下列运算正确的是( )
A、(-
| ||||
| B、(x3+1)′=3x2+1 | ||||
| C、(cosx)′=sinx | ||||
D、(log2x)′=
|
若直线x+y=m与圆x2+y2=m相切,则m的值为( )
| A、0 | B、1 | C、2 | D、0或2 |
定义方程f(x)=f′(x)的实数根x0叫做函数f(x)的“新不动点”,则下列函数有且只有一个“新不动点”的函数是( )
①g(x)=
x2;
②g(x)=-ex-2x;
③g(x)=lnx;
④g(x)=sinx+2cosx.
①g(x)=
| 1 |
| 2 |
②g(x)=-ex-2x;
③g(x)=lnx;
④g(x)=sinx+2cosx.
| A、①② | B、②③ | C、②④ | D、②③④ |
已知f(x)是定义在R上的偶函数,且在(-∞,0]是减函数,设a=f(log26),b=f(log
3),c=f(
)则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、c<b<a |
| B、b<c<a |
| C、b<a<c |
| D、a<b<c |
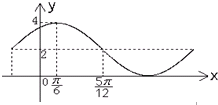 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果