题目内容
已知数列{log2(an-1)}(n∈N*)为等差数列,a1=3,a3=9,
(1)求数列{an}的通项公式.
(2)求和Sn=
+
+…+
.
(1)求数列{an}的通项公式.
(2)求和Sn=
| 1 |
| a2-a1 |
| 1 |
| a3-a2 |
| 1 |
| an+1-an |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件,能推导出{log2(an-1)}是首项为1,公差为1的等差数列,从而得到log2(an-1)=n,由此能求出数列{an}的通项公式.
(2)根据数列{an}的通项公式,先求出
,由此利用等比数列的前n项和公式能求出Sn=
+
+…+
.
(2)根据数列{an}的通项公式,先求出
| 1 |
| an+1-an |
| 1 |
| a2-a1 |
| 1 |
| a3-a2 |
| 1 |
| an+1-an |
解答:
解:(1)∵数列{log2(an-1)}(n∈N*)为等差数列,a1=3,a3=9,
∴log2(a1-1)=log22=1,
log2(a3-1)=log28=3,
∴{log2(an-1)}是首项为1,公差为1的等差数列,
∴log2(an-1)=1+n-1=n,
∴an-1=2n,
∴an=2n+1.
(2)∵an=2n+1,
∴
=
=
,
∴Sn=
+
+…+
=
+
+…+
=
=1-
.
∴log2(a1-1)=log22=1,
log2(a3-1)=log28=3,
∴{log2(an-1)}是首项为1,公差为1的等差数列,
∴log2(an-1)=1+n-1=n,
∴an-1=2n,
∴an=2n+1.
(2)∵an=2n+1,
∴
| 1 |
| an+1-an |
| 1 |
| 2n+1-2n |
| 1 |
| 2n |
∴Sn=
| 1 |
| a2-a1 |
| 1 |
| a3-a2 |
| 1 |
| an+1-an |
=
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
=
| ||||
1-
|
=1-
| 1 |
| 2n |
点评:本题考查数列的通项公式和前n项和公式的求法,解题时要熟练掌握等差数列和等比数列的性质,是中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
若直线x+y=m与圆x2+y2=m相切,则m的值为( )
| A、0 | B、1 | C、2 | D、0或2 |
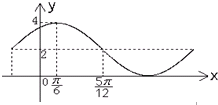 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果