题目内容
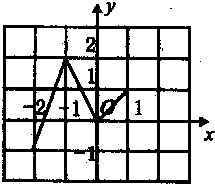 已知定义在R上的函数f(x)满足f(x)=f(x+3),如图表示 该函数在区间(-2,1]上的图象,则f(2011)+f(2012)等于( )
已知定义在R上的函数f(x)满足f(x)=f(x+3),如图表示 该函数在区间(-2,1]上的图象,则f(2011)+f(2012)等于( )| A、3 | B、2 | C、1 | D、0 |
考点:函数的周期性
专题:函数的性质及应用
分析:由f(x)=f(x+3),可知函数是周期为3的周期函数,然后利用函数的周期性即可求得结果.
解答:
解:∵定义在R上的函数f(x)满足f(x)=f(x+3),
∴函数f(x)的周期是3,
∴f(2011)+f(2012)=f(1)+f(2)=f(1)+f(-1),
由图象可知f(1)=1,f(-1)=2,
∴f(2011)+f(2012)=f(1)+f(-1)=1+2=3,
故选:A.
∴函数f(x)的周期是3,
∴f(2011)+f(2012)=f(1)+f(2)=f(1)+f(-1),
由图象可知f(1)=1,f(-1)=2,
∴f(2011)+f(2012)=f(1)+f(-1)=1+2=3,
故选:A.
点评:本题主要考查函数值的计算,利用条件求出函数的周期是解决本题的关键,要求熟练掌握函数周期的应用.

练习册系列答案
相关题目
下列运算正确的是( )
A、(-
| ||||
| B、(x3+1)′=3x2+1 | ||||
| C、(cosx)′=sinx | ||||
D、(log2x)′=
|
函数f(x)=
+(x-1)0的定义域为( )
| 1 | ||
|
A、(-
| ||
| B、(-2,1)∪(1,+∞) | ||
C、(-
| ||
| D、(0,1)∪(1,+∞) |
下列三数
,log1682,log27124的大小关系是( )
| 3 |
| 2 |
A、
| ||
B、
| ||
C、log27124<
| ||
D、log27124<log1682<
|
执行如图所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是( )


| A、66 | B、67 | C、68 | D、69 |
若直线x+y=m与圆x2+y2=m相切,则m的值为( )
| A、0 | B、1 | C、2 | D、0或2 |
 对于实数x,定义[x]表示不超过x的最大整数,执行如图的程序框图,如果输入的N=2014,则输出的[S]是( )
对于实数x,定义[x]表示不超过x的最大整数,执行如图的程序框图,如果输入的N=2014,则输出的[S]是( )