题目内容
在直角坐标系中,已知角α的终边与单位圆交点的横坐标是-
,角α+β的终边与单位圆交点的纵坐标是
,且α、β∈(0,π)则cosβ= .
| 3 |
| 5 |
| 5 |
| 13 |
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:角α终边与单位圆交点的横坐标即为cosα的值,由α+β的范围及sin(α+β)的值,利用同角三角函数间的基本关系求出cos(α+β)、sinα的值,利用两角和与差的正弦函数公式化简后,将各自的值代入计算即可求出值.
解答:
解:由题意可得cosα=-
,sin(α+β)=
,α、β∈(0,π),
∴α为钝角,α+β为钝角,
∴sinα=
,cos(α+β)=-
.
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=-
×(-
)+
×
=
,
故答案为:
.
| 3 |
| 5 |
| 5 |
| 13 |
∴α为钝角,α+β为钝角,
∴sinα=
| 4 |
| 5 |
| 12 |
| 13 |
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=-
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 4 |
| 5 |
| 56 |
| 65 |
故答案为:
| 56 |
| 65 |
点评:此题考查了两角和与差的正弦、余弦函数公式,同角三角函数间的基本关系,以及锐角三角函数定义,熟练掌握公式是解本题的关键,属于中档题.

练习册系列答案
相关题目
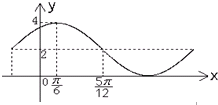 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果