题目内容
20.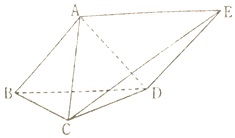 如图,在多面体ABCDE中,ABDE是平行四边形,AB、AC、AD两两垂直.
如图,在多面体ABCDE中,ABDE是平行四边形,AB、AC、AD两两垂直.(Ⅰ)求证:平面ACD⊥平面ECD;
(Ⅱ)若BC=CD=DB=$\sqrt{2}$,求点B到平面ECD的距离.
分析 (Ⅰ)由AB⊥AC,AB⊥AD,得AB⊥平面ACD,推导出AB∥DE,从而DE⊥平面ACD,由此能证明平面ACD⊥平面ECD.
(Ⅱ)连接BE.设B到平面CDE的距离为h,由VB-CDE=VE-BCD,能求出B到平面CDE的距离.
解答 证明:(Ⅰ)∵AB⊥AC,AB⊥AD,AC∩AD=A,
∴AB⊥平面ACD,
∵ABDE是平行四边形,∴AB∥DE,
∴DE⊥平面ACD,
∵DE?平面CDE,
∴平面ACD⊥平面ECD.
解:(Ⅱ)连接BE.∵AB,AC,AD两两互相垂直,$BC=CD=DB=\sqrt{2}$,
∴$A{C^2}+A{C_1}^2=A{C^2}+A{B_1}^2=A{B_1}^2+A{C_1}^2=2$,
∴AC=AC1=AB1=1,
∴${V_{B-ACD}}=\frac{1}{3}{S_{A{B_1}{C_1}}}•AB=\frac{1}{3}×\frac{1}{2}×1×1×1=\frac{1}{6}$,
∵AE∥BD,∴AE∥平面BCD,
∴${V_{E-BCD}}={V_{A-BCD}}=\frac{1}{6}$.
又由(Ⅰ)知DE⊥平面ACD,
∴DE⊥CD,∴${S_{△CDE}}=\frac{1}{2}DE•CD=\frac{1}{2}×\sqrt{2}×1=\frac{{\sqrt{2}}}{2}$.
设B到平面CDE的距离为h,
所以由VB-CDE=VE-BCD,得$\frac{1}{3}{S_{△CDE}}•h=\frac{1}{6}$,
所以$h=\frac{{\frac{1}{2}}}{{{S_{△CDE}}}}=\frac{{\sqrt{2}}}{2}$,即B到平面CDE的距离为$\frac{{\sqrt{2}}}{2}$.
点评 本题考查面面垂直的证明,考查点到平面的距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 0 | B. | 2019 | C. | -2019 | D. | 2018×2019 |
| A. | 2 | B. | -2 | C. | $±\frac{1}{2}$ | D. | ±2 |