题目内容
10．已知p：${log_2}（{{x^2}-3x}）＞2$，q：$\frac{x-4}{x+1}＞0$，则p是q的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 根据不等式的解法求出不等式的等价条件，结合充分条件和必要条件的定义进行判断即可．
解答 解：由${log_2}（{{x^2}-3x}）＞2$得x2-3x＞4，即x2-3x-4＞0，得x＞4或x＜-1，即p：x＞4或x＜-1，
由$\frac{x-4}{x+1}＞0$得：x＞4或x＜-1，即q：x＞4或x＜-1，
则p是q的充要条件，
故选：C
点评 本题主要考查充分条件和必要条件的判断，根据不等式的性质求出不等式的等价条件结合充分条件和必要条件的定义是解决本题的关键．
练习册系列答案
相关题目
1．
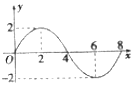已知函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，x≥0）的部分图象如图所示，则f（1）+f（2）+f（3）+…+f（11）的值等于（ ）
已知函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，x≥0）的部分图象如图所示，则f（1）+f（2）+f（3）+…+f（11）的值等于（ ）| A． | 2 | B． | $2+\sqrt{2}$ | C． | $2+2\sqrt{2}$ | D． | $-2-\sqrt{2}$ |
15．某体育彩票规定：从01到36个号中抽出7个号为一注，每注2元．某人想先选定吉利号18，然后再从01到17个号中选出3个连续的号，从19到29个号中选出2个连续的号，从30到36个号中选出1个号组成一注．若这个人要把这种要求的号全买，至少要花的钱数为（ ）
| A． | 2000元 | B． | 3200元 | C． | 1800元 | D． | 2100元 |
2．在一个口袋中装有大小相同的5个白球和3个黑球，从中摸出3个球，至少摸到2个黑球的概率为（ ）
| A． | $\frac{9}{28}$ | B． | $\frac{3}{8}$ | C． | $\frac{3}{7}$ | D． | $\frac{2}{7}$ |
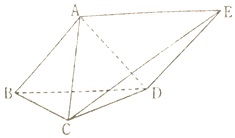如图，在多面体ABCDE中，ABDE是平行四边形，AB、AC、AD两两垂直．