题目内容
不等式
＜1的解集是 ．
| 1 |
| x-1 |
考点：其他不等式的解法
专题：计算题,不等式的解法及应用
分析：运用移项、通分和符号法，转化为一次不等式组，分别解出它们，再求并集即可．
解答：
解：不等式
＜1即为
-1＜0，
即
＜0，
即有
或
，
即
或
，
即x＜1或x＞2．
则解集为（-∞，1）∪（2，+∞）．
故答案为：（-∞，1）∪（2，+∞）．
| 1 |
| x-1 |
| 1 |
| x-1 |
即
| 2-x |
| x-1 |
即有
|
|
即
|
|
即x＜1或x＞2．
则解集为（-∞，1）∪（2，+∞）．
故答案为：（-∞，1）∪（2，+∞）．
点评：本题考查分式不等式的解法，考查转化思想的运用，考查运算能力，属于基础题和易错题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
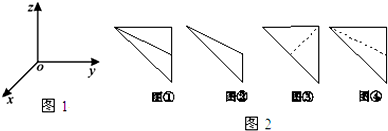
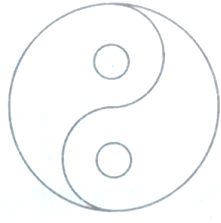给如图所示的4个区域涂上颜色，可得一个漂亮的“太极图”，现有红、黑、黄、蓝四种颜色供选用，要求每个区域只能涂一种颜色，且相邻的区域颜色不同，则有