题目内容
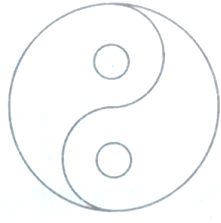 给如图所示的4个区域涂上颜色,可得一个漂亮的“太极图”,现有红、黑、黄、蓝四种颜色供选用,要求每个区域只能涂一种颜色,且相邻的区域颜色不同,则有
给如图所示的4个区域涂上颜色,可得一个漂亮的“太极图”,现有红、黑、黄、蓝四种颜色供选用,要求每个区域只能涂一种颜色,且相邻的区域颜色不同,则有考点:计数原理的应用
专题:排列组合
分析:由题意可知,需要分三类,分三类,第一类,用4种颜色,第二类,用3种颜色,第三类,用2种颜色,根据分类计数原理可得答案
解答:
 解:分三类,第一类,用4种颜色,每个区域只能涂一种颜色,有
解:分三类,第一类,用4种颜色,每个区域只能涂一种颜色,有
=24种,
第二类,用3种颜色,有
=4种,先涂A有3种选择,B也有3种选择,C有2种选择,故有4×3×3×2=72种,
第三类,用2种颜色,A与D一样,B与C一样,有
=12种,
根据分类计数原理,一共有24+72+12=108种
故答案为:108
 解:分三类,第一类,用4种颜色,每个区域只能涂一种颜色,有
解:分三类,第一类,用4种颜色,每个区域只能涂一种颜色,有| A | 4 4 |
第二类,用3种颜色,有
| C | 3 4 |
第三类,用2种颜色,A与D一样,B与C一样,有
| A | 2 4 |
根据分类计数原理,一共有24+72+12=108种
故答案为:108
点评:本题考查了分类计数原理,关键是分类,属于基础题,(若AB相同,有
=6,若AB不同,有3×2×2=12,共6+12=18,两者一样,A有3种选择,B也有3种选择,包含相同和不相同)
| A | 3 3 |

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
在如图所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(2,1,1),(2,2,2).给出编号为①,②,③,④的四个图,则该四面体的侧视图和俯视图分别为( )
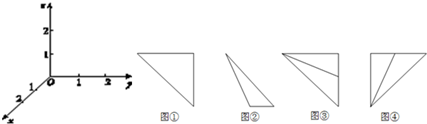

| A、①和② | B、①和③ |
| C、③和② | D、④和② |