题目内容
已知数列{an}的前n项和Sn满足Sn+1+Sn-1=2Sn+1(n≥2,n∈N*),且a1=2,a2=3.
(1)求数列{an}的通项公式;
(2)设bn=4n+(-1)n-1•λ•2an(λ为非零整数,n∈N*),求λ的值,使得对任意n∈N*,bn+1>bn恒成立.
(1)求数列{an}的通项公式;
(2)设bn=4n+(-1)n-1•λ•2an(λ为非零整数,n∈N*),求λ的值,使得对任意n∈N*,bn+1>bn恒成立.
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:(1)由Sn+1+Sn-1=2Sn+1(n≥2,n∈N*),变形为Sn+1-Sn-(Sn-Sn-1)=1,利用等差数列的通项公式即可得出.
(2)bn=4n+(-1)n-1•λ•2an=4n+(-1)n-1•λ•2n+1,要使得对任意n∈N*,bn+1>bn恒成立,只须bn+1-bn>0恒成立.化为(-1)n-1λ<2n-1.对n分为奇数偶数讨论即可得出.
(2)bn=4n+(-1)n-1•λ•2an=4n+(-1)n-1•λ•2n+1,要使得对任意n∈N*,bn+1>bn恒成立,只须bn+1-bn>0恒成立.化为(-1)n-1λ<2n-1.对n分为奇数偶数讨论即可得出.
解答:
解:(1)∵Sn+1+Sn-1=2Sn+1(n≥2,n∈N*),∴Sn+1-Sn-(Sn-Sn-1)=1,
∴an+1-an=1,且a2-a1=1.
∴数列{an}是等差数列,
∴an=2+(n-1)×1=n+1.
(2)bn=4n+(-1)n-1•λ•2an=4n+(-1)n-1•λ•2n+1,
要使得对任意n∈N*,bn+1>bn恒成立,只须bn+1-bn=4n+1-4n+(-1)n•λ•2n+2-(-1)n-1•λ•2n+1>0恒成立.
化为(-1)n-1λ<2n-1.(i)当n为奇数时,λ<2n-1恒成立,当且仅当n=1时,2n-1有最小值1,∴λ<1.
(ii)当n为偶数时,λ>-2n-1恒成立,当且仅当n=2时,-2n-1有最大值1,∴λ>-2.
综上可得:-2<λ<1,又λ为非0整数,则λ=-1.
因此存在非0整数λ=-1,使得对任意n∈N*,bn+1>bn恒成立.
∴an+1-an=1,且a2-a1=1.
∴数列{an}是等差数列,
∴an=2+(n-1)×1=n+1.
(2)bn=4n+(-1)n-1•λ•2an=4n+(-1)n-1•λ•2n+1,
要使得对任意n∈N*,bn+1>bn恒成立,只须bn+1-bn=4n+1-4n+(-1)n•λ•2n+2-(-1)n-1•λ•2n+1>0恒成立.
化为(-1)n-1λ<2n-1.(i)当n为奇数时,λ<2n-1恒成立,当且仅当n=1时,2n-1有最小值1,∴λ<1.
(ii)当n为偶数时,λ>-2n-1恒成立,当且仅当n=2时,-2n-1有最大值1,∴λ>-2.
综上可得:-2<λ<1,又λ为非0整数,则λ=-1.
因此存在非0整数λ=-1,使得对任意n∈N*,bn+1>bn恒成立.
点评:本题考查了递推式、等差数列的通项公式、数列的单调性,考查了分类讨论思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=
的对称中心是( )
| x+3 |
| x-2 |
| A、(2,3) |
| B、(2,1) |
| C、(-2,1) |
| D、(-2,3) |
若x、y满足约束条件
,则z=2x+y的最大值为( )
|
| A、12 | ||
| B、4 | ||
C、
| ||
| D、0 |
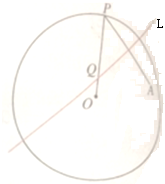 如图,圆O的半径为定长r,A是圆O内一个定点,P是圆上任意一点,线段AP的垂直平分线L和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?为什么?
如图,圆O的半径为定长r,A是圆O内一个定点,P是圆上任意一点,线段AP的垂直平分线L和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?为什么?