题目内容
9.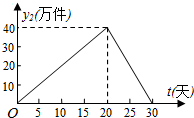 我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.
我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.| 时间t(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 日销售量y1(万件) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2与时间t所符合的函数关系式,并写出相应自变量t的取值范围;
(3)设国内、外市场的日销售总量为y万件,写出y与时间t的函数关系式,并判断上市第几天国内、外市场的日销售总量y最大,并求出此时的最大值.
分析 (1)由图可知y1与t之间是二次函数关系,设y1=a(t-0)(t-30),将已知坐标代入求出解析式;
(2)由函数图象可知y2与t之间是分段的一次函数,由t的取值范围,求出函数解析式;
(3)分段讨论函数在个点的最大值,最后再综合即可.
解答 解:(1)由图表数据观察可知y1与t之间是二次函数关系,且过(0,0),(30,0),
故设y1=a(t-0)•(t-30),
将t=5,y1=25代入解得a=-$\frac{1}{5}$,
∴y1=-$\frac{1}{5}$t(t-30)(0≤t≤30);
(2)由函数图象可知y2与t之间是分段的一次函数,由图象可知:
当0≤t<20时,y2=2t,
当20≤t≤30时,y2=-4t+120,
∴y2=$\left\{\begin{array}{l}{2t,0≤t<20}\\{-4t+120,20≤t≤30}\end{array}\right.$;
(3)分段函数分段讨论求函数最大值,过程如下:
①当0≤t<20时,y=y1+y2=-$\frac{1}{5}$t(t-30)+2t=-$\frac{1}{5}$(t-20)2+80,
图象的对称轴为t=20,当x∈(0,20]时,函数单调递增,
所以x=20时,ymax=80,
②当20≤t≤30时,y=y1+y2=-$\frac{1}{5}$t(t-30)-4t+120=-$\frac{1}{5}$(t-5)2+125,
图象的对称轴为t=5,当x∈(20,30]时,函数单调递减,
所以x=20时,ymax=80,
综合以上讨论知,上市第20天,国内、外市场的日销售总量y最大,最大值为80万件.
点评 本题主要考查了的是二次函数的应用以及分段函数的相关知识,运用形结合判断此函数是一次函数还是二次函数,属于中档题.

| A. | cos(α+β)>cosα+cosβ | B. | cos(α+β)<cosα+cosβ | ||
| C. | cos(α+β)>sinα+sinβ | D. | cos(α+β)<sinα+sinβ |
| A. | $?{x_0}∈R,{2^{x_0}}≤0$ | B. | $?{x_0}∈R,{2^{x_0}}>0$ | C. | $?{x_0}∈R,{2^{x_0}}>0$ | D. | $?{x_0}∈R,{2^{x_0}}≥0$ |