题目内容
1．若集合A={x|-1≤2x+1≤3}，B={x|$\frac{x-2}{x}$≤0}，则A∩B={x|0＜x≤1}．分析 分别求出A={x|-1≤x≤1}，B={x|0＜x≤2}，再根据交集的定义求得A∩B．
解答 解：∵A={x|-1≤2x+1≤3}，由不等式-1≤2x+1≤3解得，x∈[-1，1]，
∴A={x|-1≤x≤1}，
∵B={x|$\frac{x-2}{x}$≤0}，不等式等价为：$\left\{\begin{array}{l}{x（x-2）≤0}\\{x≠0}\end{array}\right.$，
解得x∈（0，2]，∴B={x|0＜x≤2}，
所以，A∩B={x|-1≤x≤1}∩{x|0＜x≤2}={x|0＜x≤1}，
即，A∩B={x|0＜x≤1}，
故答案为：{x|0＜x≤1}．
点评 本题主要考查了交集及其运算，涉及到一元一次不等式，分式不等式和一元二次不等式的解法，属于基础题．
练习册系列答案
相关题目
12．不等式sinx＞a在x∈（-$\frac{π}{4}$，$\frac{π}{2}$）上恒成立，则a的取值范围为（ ）
| A． | a＞1 | B． | a≤1 | C． | a≤-$\frac{\sqrt{2}}{2}$ | D． | a$≤\frac{\sqrt{2}}{2}$ |
9．
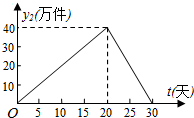我市某外资企业生产的一批产品上市后30天内全部售完，该企业对这批产品上市后每天的销售情况进行了跟踪调查．其中，国内市场的日销售量y1（万件）与时间t（t为整数，单位：天）的部分对应值如下表所示．而国外市场的日销售量y2（万件）与时间t（t为整数，单位：天）的关系如图所示．
（1）请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律，写出y1与t的函数关系式及自变量t的取值范围；
（2）分别探求该产品在国外市场上市20天前（不含第20天）与20天后（含第20天）的日销售量y2与时间t所符合的函数关系式，并写出相应自变量t的取值范围；
（3）设国内、外市场的日销售总量为y万件，写出y与时间t的函数关系式，并判断上市第几天国内、外市场的日销售总量y最大，并求出此时的最大值．
我市某外资企业生产的一批产品上市后30天内全部售完，该企业对这批产品上市后每天的销售情况进行了跟踪调查．其中，国内市场的日销售量y1（万件）与时间t（t为整数，单位：天）的部分对应值如下表所示．而国外市场的日销售量y2（万件）与时间t（t为整数，单位：天）的关系如图所示．| 时间t（天） | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 日销售量y1（万件） | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
（2）分别探求该产品在国外市场上市20天前（不含第20天）与20天后（含第20天）的日销售量y2与时间t所符合的函数关系式，并写出相应自变量t的取值范围；
（3）设国内、外市场的日销售总量为y万件，写出y与时间t的函数关系式，并判断上市第几天国内、外市场的日销售总量y最大，并求出此时的最大值．
16．下列函数中是奇函数的为（ ）
| A． | y=$\frac{{x}^{2}+cosx}{{x}^{2}-cosx}$ | B． | y=$\frac{sinx+cosx}{sinx-cosx}$ | ||
| C． | y=2cosx | D． | y=lg（sinx+$\sqrt{1+si{n}^{2}x}$） |
二次函数y=ax2+bx+c的图象如图所示，下列结论：a+b+c＞0；②a-b+c＞0；③abc＜0；④2a-b=0，其中正确的个数是（ ）
4．设命题p：?x∈R，2x＞0，则￢p为（ ）
| A． | ?x∈R，2x＜0 | B． | ?x∈R，2x＜0 | C． | ?x0∈R，2${\;}^{{x}_{0}}$≤0 | D． | ?3x0∈R，2${\;}^{{x}_{0}}$＜0 |
5．集合A={-1，5，1}，A的子集中，含有元素5的子集共有（ ）
| A． | 2个 | B． | 4个 | C． | 6个 | D． | 8个 |