题目内容
14.已知点P为抛物线y2=2x上一点,A(2,1)为定点,动点M(x,y)满足$\overrightarrow{AP}$=2$\overrightarrow{AM}$,求动点M的轨迹方程.分析 设P的坐标为P(m,n),得到$\overrightarrow{AP}$=(m-2,n-1),$\overrightarrow{AM}$=(x-2,y-1),然后根据$\overrightarrow{AP}$=2$\overrightarrow{AM}$,求出P点的坐标,进而代入抛物线方程即可得答案.
解答 解:设点P的坐标为(m,n),
则$\overrightarrow{AP}$=(m-2,n-1),$\overrightarrow{AM}$=(x-2,y-1),
∵$\overrightarrow{AP}$=2$\overrightarrow{AM}$,
∴m-2=2(x-2),n-1=2(y-1),
∴m=2x-2,n=2y-1,
即点P坐标为(2x-2,2y-1)
而点P在抛物线y2=2x上,
因此有(2y-1)2=2(2x-2),
即(y-$\frac{1}{2}$)2=x-1.
∴动点M的轨迹方程为(y-$\frac{1}{2}$)2=x-1.
点评 本题主要考查通过向量的有关运算求轨迹方程的问题.对向量的有关题型比如:求模、求夹角、求垂直以及平行等的问题一定要强化练习,是高考的热点问题.

练习册系列答案
相关题目
2.已知x>1,则y=3x+$\frac{4}{x-1}$有( )
| A. | 最大值3+4$\sqrt{3}$ | B. | 最小值3+4$\sqrt{3}$ | C. | 最大值3+2$\sqrt{3}$ | D. | 最小值3+2$\sqrt{3}$ |
9.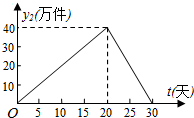 我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.
我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.
(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律,写出y1与t的函数关系式及自变量t的取值范围;
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2与时间t所符合的函数关系式,并写出相应自变量t的取值范围;
(3)设国内、外市场的日销售总量为y万件,写出y与时间t的函数关系式,并判断上市第几天国内、外市场的日销售总量y最大,并求出此时的最大值.
 我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.
我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.| 时间t(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 日销售量y1(万件) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2与时间t所符合的函数关系式,并写出相应自变量t的取值范围;
(3)设国内、外市场的日销售总量为y万件,写出y与时间t的函数关系式,并判断上市第几天国内、外市场的日销售总量y最大,并求出此时的最大值.
19.等差数列{an}的前n项和为Sn(n∈N*),且满足S15>0,S16<0,则下列选项中最大的为( )
| A. | $\frac{{S}_{6}}{{a}_{6}}$ | B. | $\frac{{S}_{7}}{{a}_{7}}$ | C. | $\frac{{S}_{9}}{{a}_{9}}$ | D. | $\frac{{S}_{8}}{{a}_{8}}$ |
 二次函数y=ax2+bx+c的图象如图所示,下列结论:a+b+c>0;②a-b+c>0;③abc<0;④2a-b=0,其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:a+b+c>0;②a-b+c>0;③abc<0;④2a-b=0,其中正确的个数是( )