Question

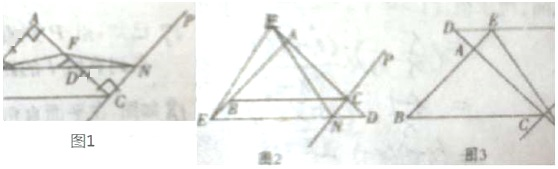
在△ABC中，∠BAC=90°，AB=AC，E为直线AB上一点，过点C作直线CP平行AB，过点E作直线EN平行BC交CP于点N，交直线AC于点D，F为直线AC上一点，且AE=CF，连接EF、FN．
（1）如图1，当点E、F分别在线段AB、AC上时，求证：△AEF≌△CFN．
（2）如图2，当点E、F分别在线段AB、CA的延长线上时，
①（1）中的结论是否成立？不必写出证明过程．
②若∠AEF=15°，EF=m，请用含m的式子表示EN的长．
（3）如图3，当点E、F分别在线段BA、AC的延长线上时，若∠NEF=a（0°＜a＜90°），EF=n，请直接用含n，a的式子表示EN的长．

Answer 1

考点：平面图形的直观图,斜二测法画直观图

专题：立体几何

分析：（1）∵在△ABC中，∠BAC=90°，AB=AC，根据CP∥AB，EN∥BC，可得△DCN，△AEF也为等腰直角三角形，进而可得AF=CN，由SAS可得：△AEF≌△CFN．
（2）如图2，当点E、F分别在线段AB、CA的延长线上时，①（1）中的结论依然成立，②进而可得EF=FN=m，又由∠AEF=15°，可得∠AEN=60°，即故△AEN为等边三角形，故EN=m．
（3）当点E、F分别在线段BA、AC的延长线上时，△AEF≌△CFN依然成立；由EF=FN=n，∠AEF=α，可得：EN=2ncosα．

解答： 证明：（1）∵在△ABC中，∠BAC=90°，AB=AC，
故△ABC为等腰直角三角形，
∵CP∥AB，EN∥BC，
故△DCN，△AEF也为等腰直角三角形，
故CD=CN，AE=AD，
又∵AE=CF，
∴AF=BE=CD=CN，
故△AEF≌△CFN．
解：（2）当点E、F分别在线段AB、CA的延长线上时，
①△AEF≌△CFN依然成立；
②∵△AEF≌△CFN，
∴EF=FN=m，
又∵∠AEF=15°，
∴∠AEN=60°，
故△AEN为等边三角形，
故EN=m．
（3）当点E、F分别在线段BA、AC的延长线上时，
△AEF≌△CFN依然成立；
∴EF=FN=n，
又∵∠AEF=α，
故EN=2ncosα．

点评：本题考查的知识点是全等三角形的证明，解三角形，难度不大，属于基础题．