题目内容
椭圆C:
+
=1(a>b>0)的左、右焦点分别为F1、F2,焦距为2c,若直线y=x-c与椭圆C在第一象限内的一个交点M满足∠F1MF2=2∠MF1F2,则该椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:在△MF1F2中,由正弦定理可得
=
=
=
,可得e=
=
=
,而cosθ=cos15°=
,即可得出.
| 2c |
| sin2θ |
| |MF2| |
| sinθ |
| |MF1| |
| sin3θ |
| 2a |
| sinθ+sin3θ |
| c |
| a |
| 2sinθcosθ |
| 4sinθ-4sin3θ |
| 1 |
| 2cosθ |
| ||||
| 4 |
解答:
解:如图所示,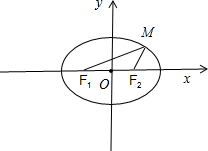
设∠MF1F2=θ.
∵tan3θ=1,
∴θ=15°.
∴cos30°=2cos215°-1,
∴cos15°=
.
在△MF1F2中,由正弦定理可得
=
=
=
,
∴e=
=
=
=
=
.
故选:D.

设∠MF1F2=θ.
∵tan3θ=1,
∴θ=15°.
∴cos30°=2cos215°-1,
∴cos15°=
| ||||
| 4 |
在△MF1F2中,由正弦定理可得
| 2c |
| sin2θ |
| |MF2| |
| sinθ |
| |MF1| |
| sin3θ |
| 2a |
| sinθ+sin3θ |
∴e=
| c |
| a |
| 2sinθcosθ |
| 4sinθ-4sin3θ |
| 1 |
| 2cosθ |
| 2 | ||||
|
| ||||
| 2 |
故选:D.
点评:本题考查了正弦定理、椭圆的定义及其性质、倍角公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
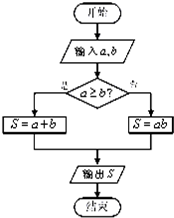 定义一种运算S=a?b,在框图所表达的算法中揭示了这种运算“?”的含义.那么,按照运算“?”的含义,计算tan15°?tan30°+tan30°?tan15°=
定义一种运算S=a?b,在框图所表达的算法中揭示了这种运算“?”的含义.那么,按照运算“?”的含义,计算tan15°?tan30°+tan30°?tan15°=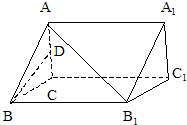 在空间平移正△ABC到△A1B1C1得到如图所示的几何体,若D是AC的中点,AA1⊥平面ABC,AA1:AB=
在空间平移正△ABC到△A1B1C1得到如图所示的几何体,若D是AC的中点,AA1⊥平面ABC,AA1:AB=