题目内容
已知正三棱柱ABC-A1B1C1中，AB1⊥BC1，求证：A1C⊥BC1．
考点：棱锥的结构特征
专题：空间位置关系与距离
分析：连结A1C，AC1交点为E，则点E是A1C的中点．取B1C1的中点D，连结A1D、DN，则DE∥AB1．求证线线垂直，往往寻求线面垂直，只要证得BC1⊥平面A1DE即可．
解答：
证明：如图所示，连结A1C，AC1交点为E，则点E是A1C的中点．．
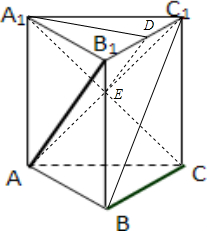
取B1C1的中点D，连结A1D、DE，则DE∥AB1．
又AB1⊥BC1，
∴DE⊥BC1，
又△A1B1C1是正三角形，
∴A1D⊥B1C1．
又平面A1B1C1⊥平面BB1C1C，平面A1B1C1∩平面BB1C1C=B1C1，A1D?平面A1B1C1，
∴A1D⊥平面BB1C1C．
又BC1?平面BB1C1C，
∴BC1⊥A1D．
又A1D?平面A1DE，DE?平面A1DE，A1D∩DE=D，
∴BC1⊥平面A1DE．
又A1C?平面A1DE，
∴A1C⊥BC1．
取B1C1的中点D，连结A1D、DE，则DE∥AB1．
又AB1⊥BC1，
∴DE⊥BC1，
又△A1B1C1是正三角形，
∴A1D⊥B1C1．
又平面A1B1C1⊥平面BB1C1C，平面A1B1C1∩平面BB1C1C=B1C1，A1D?平面A1B1C1，
∴A1D⊥平面BB1C1C．
又BC1?平面BB1C1C，
∴BC1⊥A1D．
又A1D?平面A1DE，DE?平面A1DE，A1D∩DE=D，
∴BC1⊥平面A1DE．
又A1C?平面A1DE，
∴A1C⊥BC1．
点评：本题主要考查了线面垂直的性质和判定，同时考查了空间想象能力、运算求解的能力、以及转化与划归的思想，属于中档题．
练习册系列答案
相关题目
如图，三棱锥P-ABC，底面ABC为边长为2已知数列{an}的前n项之和是Sn，且4Sn=（an+1）2，则下列说法正确的是（ ）
| A、数列{an}为等差数列 |
| B、数列{an}为等比数列 |
| C、数列{an}为等差或等比数列 |
| D、数列{an}可能既不是等差数列也不是等比数列 |
△ABC与A1、B1、C1不在同一平面内，如果三条直线AA1，BB1，CC1，两两相交，求证：AA1，BB1，CC1交于一点．