题目内容
已知椭圆
+
=1(0<b<2)的左焦点为F,左右顶点分别为A,C,上顶点为B,过F,B,C作⊙P.
(1)当b=
时,求圆心P的坐标;
(2)是否存在实数b,使得直线AB与⊙P相切?若存在求b的值,若不存在,请说明理由.
| x2 |
| 4 |
| y2 |
| b2 |
(1)当b=
| 3 |
(2)是否存在实数b,使得直线AB与⊙P相切?若存在求b的值,若不存在,请说明理由.
考点:椭圆的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)利用已知和椭圆的性质即可得出a,b,c.进而得到点B,C,F的坐标,设出圆的一般方程,利用待定系数法即可得出;
(2)假设存在实数b,使得直线AB与⊙P相切,运用圆的性质和圆的切线的性质,设圆心P(
,d),
运用垂直的条件和圆的半径相等即可判断.
(2)假设存在实数b,使得直线AB与⊙P相切,运用圆的性质和圆的切线的性质,设圆心P(
| a-c |
| 2 |
运用垂直的条件和圆的半径相等即可判断.
解答:
解:(1)当b=
时,椭圆方程为
+
=1,
∴a2=4,得a=2.∴c=
=
=1.
∴A(-2,0),B(0,
),C(2,0),F(-1,0),
设圆P的方程为x2+y2+Dx+Ey+F=0,
则
,解得
.
∴圆P的方程为x2+y2-x-
y-2=0,即有圆心P(
,
);
(2)假设存在实数b,使得直线AB与⊙P相切,则有B为切点,B(0,b),
则设圆心P(
,d),即有
=(c,b),
=(
,b-d),
=(
,-d),
由
•
=0且|
|=|
|,
则c•
+b(b-d)=0且
=
即为c2+2b2=ac+2bd且ac+2bd=b2,即有c2+b2=0,不成立.
故不存在实数b,使得直线AB与⊙P相切.
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
∴a2=4,得a=2.∴c=
| a2-b2 |
| 4-3 |
∴A(-2,0),B(0,
| 3 |
设圆P的方程为x2+y2+Dx+Ey+F=0,
则
|
|
∴圆P的方程为x2+y2-x-
| ||
| 3 |
| 1 |
| 2 |
| ||
| 6 |
(2)假设存在实数b,使得直线AB与⊙P相切,则有B为切点,B(0,b),
则设圆心P(
| a-c |
| 2 |
| AB |
| PB |
| c-a |
| 2 |
| PC |
| a+c |
| 2 |
由
| AB |
| PB |
| PB |
| PC |
则c•
| c-a |
| 2 |
(
|
(
|
即为c2+2b2=ac+2bd且ac+2bd=b2,即有c2+b2=0,不成立.
故不存在实数b,使得直线AB与⊙P相切.
点评:熟练掌握椭圆的性质、圆的切线性质及其一般方程、待定系数法是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
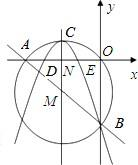 如图所示,在平面直角坐标系中,圆M经过原点O且与x轴y轴分别相交于A(-6,0),B(0,-8)两点,若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过B.
如图所示,在平面直角坐标系中,圆M经过原点O且与x轴y轴分别相交于A(-6,0),B(0,-8)两点,若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过B.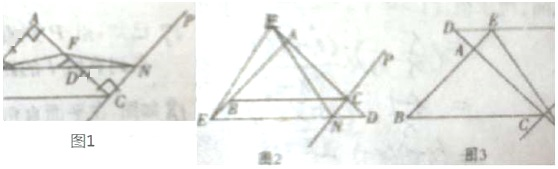
 △ABC与A1、B1、C1不在同一平面内,如果三条直线AA1,BB1,CC1,两两相交,求证:AA1,BB1,CC1交于一点.
△ABC与A1、B1、C1不在同一平面内,如果三条直线AA1,BB1,CC1,两两相交,求证:AA1,BB1,CC1交于一点.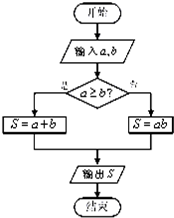 定义一种运算S=a?b,在框图所表达的算法中揭示了这种运算“?”的含义.那么,按照运算“?”的含义,计算tan15°?tan30°+tan30°?tan15°=
定义一种运算S=a?b,在框图所表达的算法中揭示了这种运算“?”的含义.那么,按照运算“?”的含义,计算tan15°?tan30°+tan30°?tan15°=