题目内容
 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,AD=
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,AD=| 3 |
(1)求三棱锥E-PAD的体积;
(2)证明:无论点E在边BC的何处,都有PE⊥AF.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)求出三棱锥E-PAD的高为1,运用体积公式求解即可,(2)转化证明AF⊥面PBC,即可得证PE⊥AF.
解答:
解:(1)∵底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,AD=
,点E在边BC上移动.
∴三棱锥E-PAD的高为1
∴三棱锥E-PAD的体积=
×
×AD×AP×AB=
×
×
×1×1=
,

(2)证明:∵四边形ABCD是矩形,PA⊥平面ABCD,
∴BC⊥面PAB,
∵AF?面PAB,
∴BC⊥AF,
∵点F是PB的中点,PA=AB=1,
∴AF⊥PB,
∵PB∩BC=B
∴AF⊥面PBC,
∵PE?面PBC,
∴PE⊥AF.
| 3 |
∴三棱锥E-PAD的高为1
∴三棱锥E-PAD的体积=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 6 |

(2)证明:∵四边形ABCD是矩形,PA⊥平面ABCD,
∴BC⊥面PAB,
∵AF?面PAB,
∴BC⊥AF,
∵点F是PB的中点,PA=AB=1,
∴AF⊥PB,
∵PB∩BC=B
∴AF⊥面PBC,
∵PE?面PBC,
∴PE⊥AF.
点评:本题考查了空间几何体的体积计算,几何体中的直线,平面的垂直问题,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 如图所示,已知三棱锥P-ABC中,∠ACB=90°,BC=4,AB=20,D为AB的中点,且△PDB是等边三角形,PA⊥PC.
如图所示,已知三棱锥P-ABC中,∠ACB=90°,BC=4,AB=20,D为AB的中点,且△PDB是等边三角形,PA⊥PC.
 已知:如图,点B是AD的中点,点E是AB的中点,AB=AC.求证:CE=
已知:如图,点B是AD的中点,点E是AB的中点,AB=AC.求证:CE=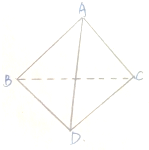 如图,三棱锥A-BCD中,DC⊥BC,BC=2
如图,三棱锥A-BCD中,DC⊥BC,BC=2