题目内容
若存在x∈[-2，3]，使不等式2x-x2≥a成立，则实数a的取值范围是（ ）
| A、（-∞，1] |
| B、（-∞，-8] |
| C、[1，+∞） |
| D、[-8，+∞） |
考点：二次函数的性质
专题：函数的性质及应用
分析：由条件利用二次函数的性质求得函数f（x）=2x-x2在∈[-2，3]上的最大值，可得a的范围．
解答：
解：当x∈[-2，3]时，函数f（x）=2x-x2=-（x-1）2+1，
故当x=1时，f（x）取得最大值为1．
由于存在x∈[-2，3]，使不等式2x-x2≥a成立，∴a≤1，
故选：A．
故当x=1时，f（x）取得最大值为1．
由于存在x∈[-2，3]，使不等式2x-x2≥a成立，∴a≤1，
故选：A．
点评：本题主要考查求二次函数在闭区间上的最值，二次函数的性质的应用，属于基础题．
练习册系列答案
相关题目
执行如图所示程序，输出S的值为（ ）
| A、8 | B、26 | C、170 | D、42 |
下列说法正确的是（ ）
①若a，b，c∈R且ac2＞bc2，则a＞b；
②若a，b∈R且a＞b，则a3＞b3；
③若a，b∈R且ab≠0，则
+
≥2；
④函数f（x）=x+
（x≠0）的最小值是2．
①若a，b，c∈R且ac2＞bc2，则a＞b；
②若a，b∈R且a＞b，则a3＞b3；
③若a，b∈R且ab≠0，则
| a |
| b |
| b |
| a |
④函数f（x）=x+
| 1 |
| x |
| A、①② | B、②③ | C、③④ | D、①④ |
函数f（x）=2x2-lnx的递减区间是（ ）
A、（0，
| ||||
B、（-
| ||||
C、（
| ||||
D、（-∞，-
|
二进制数110011（2）转化为十进制数为（ ）
| A、51 | B、50 | C、49 | D、19 |
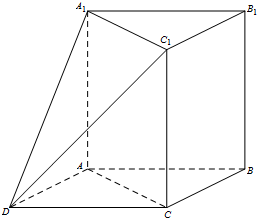如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠ACB=90°．以AB，BC为邻边作平行四边形ABCD，连接DA1和DC1．