题目内容
在极坐标系中与圆ρ=4sin(θ+
)相切的一条直线的方程为( )
| π |
| 4 |
A、ρsin(θ-
| ||
| B、ρsinθ=4 | ||
| C、ρcosθ=4 | ||
D、ρcos(θ-
|
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把圆的极坐标方程化为直角坐标方程,求出圆心和半径,再求出圆心到各个选项中直线的距离,将他和半径作对比,可得结论.
解答:
解:圆ρ=4sin(θ+
)即 ρ2=2
ρcosθ+2
ρsinθ,
化为直角坐标方程为 (x-
)2+(y-
)2=4,表示以(
,
)为圆心,半径等于2的圆.
而 ρsin(θ-
)=4,即
x-
y+8=0,圆心(
,
)到直线的距离为
=4,大于半径,
故此直线和圆相离,故排除A.
由于ρsinθ=4 即 y=4 显然它和圆相离,故排除B.
由于ρcosθ=4即 x=4,显然它和圆相离,故排除C.
由于ρcos(θ-
)=4,即
x+
y-8=0,圆心(
,
)到直线的距离为
=2,正好等于半径,
故直线和圆相切,故满足条件.
故选:D.
| π |
| 4 |
| 2 |
| 2 |
化为直角坐标方程为 (x-
| 2 |
| 2 |
| 2 |
| 2 |
而 ρsin(θ-
| π |
| 4 |
| 2 |
| 2 |
| 2 |
| 2 |
| |2-2+8| | ||
|
故此直线和圆相离,故排除A.
由于ρsinθ=4 即 y=4 显然它和圆相离,故排除B.
由于ρcosθ=4即 x=4,显然它和圆相离,故排除C.
由于ρcos(θ-
| π |
| 4 |
| 2 |
| 2 |
| 2 |
| 2 |
| |2+2-8| | ||
|
故直线和圆相切,故满足条件.
故选:D.
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,属于基础题.

练习册系列答案
相关题目
 如图,过椭圆
如图,过椭圆| x2 |
| 3 |
| A、6 | ||
| B、12 | ||
C、2
| ||
D、4
|
在平面直角坐标系xOy中,设双曲线
-
=1(a>0,b>0)的左焦点为F,圆M的圆心M在y轴正半轴上,半径为双曲线的实轴长2a,若圆M与双曲线的两渐近线均相切,且直线MF与双曲线的一条渐近线垂直,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
执行如图所示程序,输出S的值为( )


| A、8 | B、26 | C、170 | D、42 |
一个袋中装有大小相同的5个白球和3个红球,现在不放回的取2次球,每次取出一个球,记“第1次拿出的是白球”为事件A,“第2次拿出的是白球”为事件B,则事件A与B同时发生的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若抛物线x2=2py(p>0)的焦点与双曲线
-x2=1的一个焦点重合,则p的值为( )
| y2 |
| 3 |
| A、-2 | B、2 | C、-4 | D、4 |
 如图,在△ABC中,M,N是AB的三等分点,E,F是AC的三等分点,若BC=1,则ME+NF=
如图,在△ABC中,M,N是AB的三等分点,E,F是AC的三等分点,若BC=1,则ME+NF=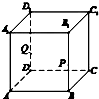 已知如图所示的正方体ABCD-A1B1C1D1,点P、Q分别在棱BB1、DD1上,且
已知如图所示的正方体ABCD-A1B1C1D1,点P、Q分别在棱BB1、DD1上,且