题目内容
二次函数y=x2(x>0)的图象在点(an,an2)处的切线与x轴交点的横坐标为an+1,n为正整数,a1=
,则S5=( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:利用导数研究曲线上某点切线方程,数列与函数的综合
专题:计算题,导数的概念及应用
分析:求出导数,求出切线的斜率,由点斜式方程得到切线方程,再令y=0,得到an+1=
an,再由等比数列的求和公式,即可得到S5.
| 1 |
| 2 |
解答:
解:函数y=x2(x>0)的导数为y′=2x,
则在点(an,an2)处的切线方程为:y-an2=2an(x-an),
当y=0时,解得x=
an,
∴an+1=
an,即数列{an}是等比数列,公比q为
,
∵a1=
,∴S5=
=
•[1-(
)5].
故选C.
则在点(an,an2)处的切线方程为:y-an2=2an(x-an),
当y=0时,解得x=
| 1 |
| 2 |
∴an+1=
| 1 |
| 2 |
| 1 |
| 2 |
∵a1=
| 1 |
| 3 |
| ||||
1-
|
| 2 |
| 3 |
| 1 |
| 2 |
故选C.
点评:本题考查导数的几何意义,等比数列的求和公式和应用,解题时要灵活地运用函数的切线方程,合理地进行等价转换.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
椭圆
+
=1与双曲线
-
=1有相同的焦点,则实数a的值是( )
| x2 |
| 6 |
| y2 |
| a2 |
| x2 |
| a |
| y2 |
| 4 |
A、
| ||
| B、1或-2 | ||
C、1或
| ||
| D、1 |
已知直线l1:(1-a)x+ay-2=0,l2:ax+(2a+1)y+3=0,若l1⊥l2,则a的值为( )
| A、0 | B、-2 |
| C、-2或0 | D、0或2 |
三棱锥的三个侧面都是直角三角形,且三个直角的顶点恰是三棱锥的顶点,则其底面一定是( )
| A、直角三角形 |
| B、钝角三角形 |
| C、锐角三角形 |
| D、等边三角形 |
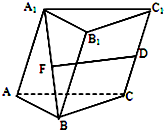
在三棱柱ABC-A1B1C1中,D是CC1的中点,F是A1B的中点,且
=α
+β
,则( )
| DF |
| AB |
| AC |

A、α=
| ||
B、α=-
| ||
C、α=1,β=-
| ||
D、α=-1,β=
|
在独立性检验中,统计量x2有两个临界值:3.841和6.635;当x2>3.841时,有95%的把握说明两个事件有关,当x2>6.635时,有99%的把握说明两个事件相关,当x2≤3.841时,认为两个事件无关.在一项调查某种药是否对心脏病有治疗作用时,共调查了3000人,经计算的x2=4.56,根据这一数据分析,认为此药物与心脏病之间( )
| A、有95%的把握认为两者相关 |
| B、约有95%的心脏病患者使用药物有作用 |
| C、有99%的把握认为两者相关 |
| D、约有99%的心脏病患者使用药物有作用 |
(x-1)4的展开式中x3的系数为( )
| A、4 | B、-4 | C、6 | D、-6 |
阅读右侧程序框图,输出结果S的值为( )


A、
| ||||
B、
| ||||
C、-
| ||||
D、
|