题目内容
三棱锥的三个侧面都是直角三角形，且三个直角的顶点恰是三棱锥的顶点，则其底面一定是（ ）
| A、直角三角形 |
| B、钝角三角形 |
| C、锐角三角形 |
| D、等边三角形 |
考点：棱锥的结构特征
专题：空间位置关系与距离
分析：借助于三角形的余弦定理判定底面三角形的形状．
解答：
解：设三条侧棱的长度分别为a，b，c，
∵三棱锥的三个侧面都是直角三角形，且三个直角的顶点恰是三棱锥的顶点，
∴底面的三条边的平方分别为a2+b2，a2+c2，b2+c2，
∴a2+b2+a2+c2-（b2+c2）=2a2＞0，a2+b2+b2+c2-a2-c2=2b2＞0，b2+c2+a2+c2-b2-a2=2c2＞0，
根据余弦定理可知，底面的三个内角都是锐角，所以底面一定是锐角三角形；
故选C．
∵三棱锥的三个侧面都是直角三角形，且三个直角的顶点恰是三棱锥的顶点，
∴底面的三条边的平方分别为a2+b2，a2+c2，b2+c2，
∴a2+b2+a2+c2-（b2+c2）=2a2＞0，a2+b2+b2+c2-a2-c2=2b2＞0，b2+c2+a2+c2-b2-a2=2c2＞0，
根据余弦定理可知，底面的三个内角都是锐角，所以底面一定是锐角三角形；
故选C．
点评：本题考查了三棱锥的性质以及利用余弦定理判定三角形的形状．
练习册系列答案
相关题目
若复数z满足zi=1+i，则z等于（ ）
| A、1-i | B、-1-i |
| C、-1+i | D、1+i |
已知sinθ=
，cosθ=
，若θ为第二象限角，则下列结论正确的是（ ）
| 1-a |
| 1+a |
| 3a-1 |
| 1+a |
A、a∈(-1，
| ||
| B、a=1 | ||
C、a=1或a=
| ||
D、a=
|
若函数h（x）=2x-k（
+1）在（1，+∞）上是增函数，则实数k的取值范围是（ ）
| 1 |
| x |
| A、[-2，+∞） |
| B、[2，+∞） |
| C、（-∞，-2] |
| D、（-∞，2] |
二次函数y=x2（x＞0）的图象在点（an，an2）处的切线与x轴交点的横坐标为an+1，n为正整数，a1=
，则S5=（ ）
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
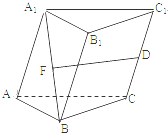在三棱柱ABC-A1B1C1中，D是CC1的中点，F是A1B的中点，且| DF |
| AB |
| AC |
A、α=
| ||
B、α=-
| ||
C、α=1，β=-
| ||
D、α=-1，β=
|
5人站成一排，甲、乙两人之间恰有1人的不同站法的种数为（ ）
| A、18 | B、24 | C、36 | D、48 |
如图所示，fi（x）（i=1，2，3，4）是定义在[0，1]上的四个函数，其中满足性质：“对[0，1]中任意的x1和x2，任意λ∈[0.1]，f[λx1+（1-λ）x2]≤λf（x1）+（1-λ）f（x2）恒成立”的只有（ ）
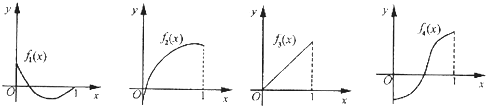
| A、f1（x），f3（x） |
| B、f2（x） |
| C、f2（x），f3（x） |
| D、f4（x） |