题目内容
如图,在△ABC中,AB=AC,AD⊥BC,且AD=1,则
•
的值是 .
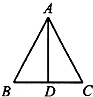
| AB |
| AD |

考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:运用向量的数量积的定义,结合解直角三角形的锐角三角函数的定义,计算即可得到结论.
解答:
解:在△ABC中,AB=AC,AD⊥BC,且AD=1,
则有ABcos∠BAD=AD=1,
即有
•
=|
|•|
|•cos∠BAD
=|
|•(|
|•cos∠BAD)=|
|2=1.
故答案为:1.
则有ABcos∠BAD=AD=1,
即有
| AB |
| AD |
| AB |
| AD |
=|
| AD |
| AB |
| AD |
故答案为:1.
点评:本题考查向量的数量积的定义,运用锐角三角函数的定义是解题的关键,属于基础题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
若x,y满足
且z=ax+2y仅在点(3,4)处取得最小值,则a的取值范围是( )
|
| A、[-4,+∞) |
| B、(-4,+∞) |
| C、(-∞,-4] |
| D、(-∞,-4) |
设x,y满足约束条件
,则z=3x+2y的最大值为( )
|
| A、8 | B、9 | C、28 | D、29 |
设x,y满足约束条件
,则
的取值范围是( )
|
| x+y+2 |
| x+1 |
| A、[1,5] |
| B、[2,6] |
| C、[2,10] |
| D、[3,11] |
设实数列{an}和{bn}分别为等差数列与等比数列,且a1=b1=8,a4=b4=1,则以下结论正确的是( )
| A、a2>b2 |
| B、a3<b3 |
| C、a5>b5 |
| D、a6>b6 |