题目内容
求数列1,x,x2,…,xn-1的前n项和.
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:分x=1,x=0和x≠1三种情况讨论,x=1时为常数列,当x=1时Sn=1,当x≠1时利用等比数列的求和公式得答案.
解答:
解:令Sn=1+x+x2+…+xn-1,
当x=1时,Sn=n;
当x=0时,Sn=1;
当x≠0且x≠1时,Sn=
.
∴数列1,x,x2,…,xn-1的前n项和Sn=
.
当x=1时,Sn=n;
当x=0时,Sn=1;
当x≠0且x≠1时,Sn=
| 1•(1-xn) |
| 1-x |
∴数列1,x,x2,…,xn-1的前n项和Sn=
|
点评:本题考查了等比数列的前n项和,考查了分类讨论的数学思想方法,是中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
已知随机变量ξ服从正态分布N(μ,δ2),且P(ξ<1)=0.5,P(ξ>2)=0.4,则P(0<ξ<1)=( )
| A、0.4 | B、0.3 |
| C、0.2 | D、0.1 |
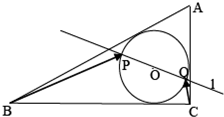 如图,圆O为Rt△ABC的内切圆,已AC=3,BC=4,AB=5,过圆心O的直线l交圆O于P、Q两点,则
如图,圆O为Rt△ABC的内切圆,已AC=3,BC=4,AB=5,过圆心O的直线l交圆O于P、Q两点,则