Question

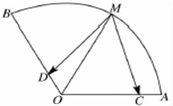如图，扇形AOB的弧的中点为M，动点C、D分别在OA、OB上，且OC=BD，OA=1，∠AOB=120．
（1）若点D是线段OB靠近点O的四分之一分点，用

OA

、

OB

表示向量

MC

；
（2）求

MC

•

MD

的取值范围．

Answer 1

考点：平面向量数量积的运算

专题：平面向量及应用

分析：（Ⅰ）连结MB，MA，由题设条件得到四边形OAMB是平行四边形，由此能求出

MC

．
（Ⅱ）设

| OC |

| OA |

=k，则

MC

=（k-1）

OA

-

OB

，

MD

=-

OA

-k

OB

，由此结合题设条件，利用向量的数量积能求出

MC

•

MD

的取值范围．

解答： 解：（I）连结MB，MA，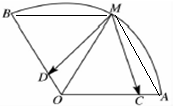
∵扇形AOB的弧的中点为M，动点C、D分别在OA、OB上，
且OC=BD，OA=1，∠AOB=120，
∴四边形OAMB是平行四边形，
∵点D是线段OB靠近点O的四分之一分点，
∴

MC

=

MA

+

AC

=

BO

+

1

4

AO

=-

1

4

OA

-

OB

．（4分）
（II）设

| OC |

| OA |

=k，则

MC

=（k-1）

OA

-

OB

，

MD

=-

OA

-k

OB

MC

•

MD

=

1

2

[(k-

1

2

)2+

3

4

]，
∵OC=BD，
∴k∈[0，

1

2

]，
∴

MC

•

MD

的取值范围是[

3

8

，

1

2

]．（6分）

点评：本题考查向量的表示，考查向量数量积的取值范围的求法，是中档题，解题时要认真审题，注意数形结合思想的合理运用．