题目内容
是否存在常数k∈R,使得函数f(x)=x4+(2-k)x2+(2-k)在(-∞,-1)上是减函数,且在[-1,0]上是增函数?若存在,请求出k的值,若不存在,请说明理由.
考点:函数单调性的性质
专题:导数的综合应用
分析:根据函数f(x)在(-∞,-1)上是减函数,且在[-1,0]上是增函数,得到x=-1是函数f(x)的一个极小值,即f'(-1)=0,然后利用导数和极值之间的关系即可得到结论.
解答:
解:要使函数f(x)在(-∞,-1)上是减函数,且在[-1,0]上是增函数,
则x=-1是函数f(x)的一个极小值,即f'(-1)=0,
∵f(x)=x4+(2-k)x2+(2-k),
∴f'(x)=4x3+2(2-k)x,
由f'(-1)=-4-2(2-k)=0,
解得k=4,
此时f'(x)=4x3-4x=4x(x2-1),
由f'(x)=4x(x2-1)>0得x>1或-1<x<0,此时函数单调递增,
由f'(x)=4x(x2-1<0得x<-1或0<x<1,此时函数单调递减,满足条件.
故存在k=4,满足条件.
则x=-1是函数f(x)的一个极小值,即f'(-1)=0,
∵f(x)=x4+(2-k)x2+(2-k),
∴f'(x)=4x3+2(2-k)x,
由f'(-1)=-4-2(2-k)=0,
解得k=4,
此时f'(x)=4x3-4x=4x(x2-1),
由f'(x)=4x(x2-1)>0得x>1或-1<x<0,此时函数单调递增,
由f'(x)=4x(x2-1<0得x<-1或0<x<1,此时函数单调递减,满足条件.
故存在k=4,满足条件.
点评:本题主要考查导数和极值之间的关系的应用,要求熟练掌握导数的公式以及函数性质和导数之间的关系.

练习册系列答案
相关题目
如果输入n=3,那么执行如图中算法的结果是( )


| A、输出3 |
| B、输出4 |
| C、输出5 |
| D、程序出错,输不出任何结果 |
已知命题p:x∈(-∞,0),3x>5x;命题q:x∈(0,
),tanx<sinx,则下列命题为真命题的是( )
| π |
| 2 |
| A、p∧q | B、¬p∨q |
| C、(¬p)∧q | D、p∧(¬q) |
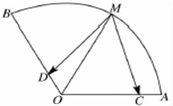 如图,扇形AOB的弧的中点为M,动点C、D分别在OA、OB上,且OC=BD,OA=1,∠AOB=120.
如图,扇形AOB的弧的中点为M,动点C、D分别在OA、OB上,且OC=BD,OA=1,∠AOB=120.