题目内容
已知动圆C经过点A(2,-3)和B(-2,-5).
(Ⅰ)若圆C的圆心在直线3x+y+5=0上,求圆C的方程;
(Ⅱ)若圆心C在x轴上,且使得三角形ABC面积为5,求圆C的方程.
(Ⅰ)若圆C的圆心在直线3x+y+5=0上,求圆C的方程;
(Ⅱ)若圆心C在x轴上,且使得三角形ABC面积为5,求圆C的方程.
考点:圆的标准方程
专题:计算题,直线与圆
分析:(I)设圆C的方程为(x-a)2+(y-b)2=r2,根据题意建立关于a、b、r的方程组,解之即可得出圆C的方程;
(II)设圆心C(a,0),利用点到直线的距离公式与三角形的面积公式,结合两点间的距离公式加以计算,可得a=13或a=3,从而得到所求圆C的方程.
(II)设圆心C(a,0),利用点到直线的距离公式与三角形的面积公式,结合两点间的距离公式加以计算,可得a=13或a=3,从而得到所求圆C的方程.
解答:
解:(Ⅰ)设所求圆C的方程为(x-a)2+(y-b)2=r2,
根据已知条件得
⇒
.
∴圆C的方程为(x+1)2+(y+2)2=10;
(Ⅱ)∵圆心C在x轴上,∴设圆心C(a,0),
∵|AB|=
=2
,
且直线AB的方程为
=
,即x-2y-8=0
∴点C到直线AB的距离d=
,
可得S△ABC=
|AB|d=
×2
×
=5,解得a=13或a=3,
∴圆C的方程为(x-13)2+y2=130或(x-3)2+y2=10.
根据已知条件得
|
|
∴圆C的方程为(x+1)2+(y+2)2=10;
(Ⅱ)∵圆心C在x轴上,∴设圆心C(a,0),
∵|AB|=
| (-2-2)2+(-5+3)2 |
| 5 |
且直线AB的方程为
| y+3 |
| -5+3 |
| x+2 |
| 2+2 |
∴点C到直线AB的距离d=
| |a-8| | ||
|
可得S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| |a-8| | ||
|
∴圆C的方程为(x-13)2+y2=130或(x-3)2+y2=10.
点评:本题给出圆C经过两个定点且圆心在定直线上,求圆的方程并依此解决三角形的面积问题.着重考查了直线的基本量与基本形式、圆的标准方程、点到直线的距离公式等知识,属于中档题.

练习册系列答案
相关题目
已知命题p:x∈(-∞,0),3x>5x;命题q:x∈(0,
),tanx<sinx,则下列命题为真命题的是( )
| π |
| 2 |
| A、p∧q | B、¬p∨q |
| C、(¬p)∧q | D、p∧(¬q) |
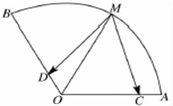 如图,扇形AOB的弧的中点为M,动点C、D分别在OA、OB上,且OC=BD,OA=1,∠AOB=120.
如图,扇形AOB的弧的中点为M,动点C、D分别在OA、OB上,且OC=BD,OA=1,∠AOB=120.