题目内容
（自选模块）
（Ⅰ）求函数f（x）=
+
，（x∈R）的最小值．
（Ⅱ）已知m，n∈R，a，b∈R+，n2m2＞a2m2+b2n2，证明：
＞a+b．
（Ⅰ）求函数f（x）=
| 3 |
| 2sin2x+1 |
| 8 |
| 3cos2x+2 |
（Ⅱ）已知m，n∈R，a，b∈R+，n2m2＞a2m2+b2n2，证明：
| m2+n2 |
考点：不等式的证明
专题：综合题,选作题,不等式的解法及应用
分析：（Ⅰ）f（x）=
+
=
+
，利用柯西不等式求最值；
（Ⅱ）n2m2＞a2m2+b2n2，变形为1＞
+
，再利用“1”的代换，结合基本不等式，即可得证．
| 3 |
| 2sin2x+1 |
| 8 |
| 3cos2x+2 |
| 9 |
| 6sin2x+3 |
| 16 |
| 6cos2x+4 |
（Ⅱ）n2m2＞a2m2+b2n2，变形为1＞
| a2 |
| n2 |
| b2 |
| m2 |
解答：
（Ⅰ）解：f（x）=
+
=
+
=
[（6sin2x+3）+（6cos2x+4）]（
+
）≥
•(3+4)2=
，
当且仅当tanx=±
时取等号，函数取得最小值为
；
（Ⅱ）证明：∵m，n∈R，a，b∈R+，n2m2＞a2m2+b2n2，
∴1＞
+
，
∴m2+n2＞（
+
）（m2+n2）＞（a+b）2，
∴
＞a+b．
| 3 |
| 2sin2x+1 |
| 8 |
| 3cos2x+2 |
| 9 |
| 6sin2x+3 |
| 16 |
| 6cos2x+4 |
=
| 1 |
| 13 |
| 9 |
| 6sin2x+3 |
| 16 |
| 6cos2x+4 |
| 1 |
| 13 |
| 49 |
| 13 |
当且仅当tanx=±
| ||
| 2 |
| 49 |
| 13 |
（Ⅱ）证明：∵m，n∈R，a，b∈R+，n2m2＞a2m2+b2n2，
∴1＞
| a2 |
| n2 |
| b2 |
| m2 |
∴m2+n2＞（
| a2 |
| n2 |
| b2 |
| m2 |
∴
| m2+n2 |
点评：本题考查柯西不等式求最值，考查基本不等式证明不等式，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
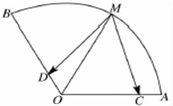如图，扇形AOB的弧的中点为M，动点C、D分别在OA、OB上，且OC=BD，OA=1，∠AOB=120．