题目内容
正实数x，y，z满足9xyz+xy+yz+zx=4，求证：
（1）xy+yz+zx≥
；
（2）x+y+z≥2．
（1）xy+yz+zx≥
| 4 |
| 3 |
（2）x+y+z≥2．
考点：基本不等式
专题：不等式的解法及应用
分析：（1）记t=
，由于x，y，z＞0．利用平均不等式xyz=(
)
≤(
)
，化简整理即可得出．（2）利用（x+y+z）2≥3（xy+yz+zx）=4，即可得出．
|
| 3 | xy•yz•xz |
| 3 |
| 2 |
| xy+yz+zx |
| 3 |
| 3 |
| 2 |
解答：
证 （1）记t=
，∵x，y，z＞0．
由平均不等式xyz=(
)
≤(
)
于是4=9xyz+xy+yz+xz≤9t3+3t2，
∴（3t-2）（3t2+3t+2）≥0，而3t2+3t+2＞0，
∴3t-2≥0，即t≥
．
∴xy+yz+zx≥
．
（2）又∵（x+y+z）2≥3（xy+yz+zx）=4，x，y，z＞0．
∴x+y+z≥2．
|
由平均不等式xyz=(
| 3 | xy•yz•xz |
| 3 |
| 2 |
| xy+yz+zx |
| 3 |
| 3 |
| 2 |
于是4=9xyz+xy+yz+xz≤9t3+3t2，
∴（3t-2）（3t2+3t+2）≥0，而3t2+3t+2＞0，
∴3t-2≥0，即t≥
| 2 |
| 3 |
∴xy+yz+zx≥
| 4 |
| 3 |
（2）又∵（x+y+z）2≥3（xy+yz+zx）=4，x，y，z＞0．
∴x+y+z≥2．
点评：本题考查了均值不等式的应用，属于基础题．
练习册系列答案
培优三好生系列答案
相关题目
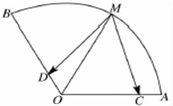如图，扇形AOB的弧的中点为M，动点C、D分别在OA、OB上，且OC=BD，OA=1，∠AOB=120．