题目内容
若抛物线y2=-2px(p>0)上有一点M,其横坐标为-9,它到焦点的距离为10,求抛物线方程和M点坐标.
考点:抛物线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:依题意,知抛物线y2=-2px(p>0)的准线方程为x=
,设M(-9,m),利用抛物线的定义,将它到焦点的距离转化为它到其焦点的距离,从而可得答案.
| p |
| 2 |
解答:
解:∵抛物线y2=-2px(p>0)的准线方程为x=
,设M(-9,m),
∵点M到焦点的距离为10,
∴由抛物线的定义知:
-(-9)=10,
解得:p=2,
∴抛物线方程为:y2=-4x;
将M(-9,m)点的坐标代入抛物线方程得:m2=-4×(-9)=36,
∴m=±6,
∴M点的坐标为(-9,-6)或(-9,6).
| p |
| 2 |
∵点M到焦点的距离为10,
∴由抛物线的定义知:
| p |
| 2 |
解得:p=2,
∴抛物线方程为:y2=-4x;
将M(-9,m)点的坐标代入抛物线方程得:m2=-4×(-9)=36,
∴m=±6,
∴M点的坐标为(-9,-6)或(-9,6).
点评:本题考查抛物线的标准方程,着重考查抛物线的概念,考查转化思想、分类讨论思想与运算求解能力,属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
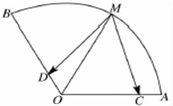 如图,扇形AOB的弧的中点为M,动点C、D分别在OA、OB上,且OC=BD,OA=1,∠AOB=120.
如图,扇形AOB的弧的中点为M,动点C、D分别在OA、OB上,且OC=BD,OA=1,∠AOB=120.