题目内容
13．已知角α的终边经过点P（2，m）（m＞0），且cosα=$\frac{2\sqrt{5}}{5}$，则m=1．分析 由条件利用任意角的三角函数的定义，求得m的值．
解答 解：∵角α的终边经过点P（2，m）（m＞0），
且cosα=$\frac{2}{\sqrt{4{+m}^{2}}}$=$\frac{2\sqrt{5}}{5}$，则m=1，
故答案为：1．
点评 本题主要考查任意角的三角函数的定义，属于基础题．
练习册系列答案
相关题目
4．如果函数f（x）=sinωx+$\sqrt{3}$cosωx的两个相邻零点间的距离为2，那么f（1）+f（2）+f（3）+…+f（9）的值为（ ）
| A． | 1 | B． | -1 | C． | $\sqrt{3}$ | D． | -$\sqrt{3}$ |
8．某学校为了解学生的学习、生活等情况，决定召开一次学生座谈会．此学校各年级人数情况如表：
（1）若按年级用分层抽样的方法抽取n个人，其中高二年级22人，高三年级20人，再从这n个人中随机抽取出1人，此人为高三年级的概率为$\frac{10}{33}$，求x、y的值．
（2）若按性别用分层抽样的方法在高三年级抽取一个容量为5的样本，从这5人中任取2人，求至少有1人是男生的概率．
| 年 级 性 别 | 高一年级 | 高二年级 | 高三年级 |
| 男 | 520 | y | 400 |
| 女 | x | 610 | 600 |
（2）若按性别用分层抽样的方法在高三年级抽取一个容量为5的样本，从这5人中任取2人，求至少有1人是男生的概率．
5．过A（0，1），B（3，5）两点的直线的斜率是（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $-\frac{4}{3}$ | D． | $-\frac{3}{4}$ |
2．已知函数y=f（2x）+2x是偶函数，且f（2）=1，则f（-2）=（ ）
| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
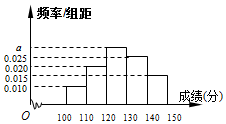某学校对高二年级期中考试数学成绩进行分析，随机抽取了分数在[100，150]的1000名学生的成绩，并根据这1000名学生的成绩画出频率分布直方图（如图所示），则成绩在[120，130）内的学生共有300人．