题目内容
已知函数f（x）=
，则f（f（2014））=（ ）
|
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
考点：函数的值
专题：函数的性质及应用
分析：根据2014＞2000，将x=2014代入x＞2000段的解析式求出f（2014）=16，再将16代入x≤2000段的解析式求出值．
解答：
解：∵f（x）=
，
∴f（f（2014））=f（16）=2cos
=2cos
=-1．
故选D．
|
∴f（f（2014））=f（16）=2cos
| 16π |
| 3 |
| 4π |
| 3 |
故选D．
点评：本题考查分段函数求值：关键是判定出自变量的值属于那一段，将自变量代入相应段的解析式，属于基础题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
已知f（x）=cos2（x-
），若f（α）=p，则f（-α）=q，则下列等式一定成立的是（ ）
| π |
| 4 |
| A、p-q=0 |
| B、p+q=0 |
| C、p+q-1=0 |
| D、p-q+1=0 |
某几何体的三视图（单位：cm）如图所示，则该几何体最长的一条侧棱长度是（ ）| A、5cm | ||
B、
| ||
C、
| ||
D、
|
在△ABC中，内角A，B，C的对边分别为a，b，c，若sin2B-sin2C=
sinCsinA，a=2
c，则B=（ ）
| 3 |
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
某同学在电脑上打下了一串黑白圆，如图所示，按这种规律往下排，那么第36个圆的颜色应是（ ）| A、黑色 | B、白色 |
| C、白色可能性大 | D、黑色可能性大 |
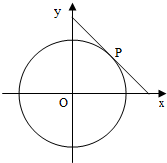圆x2+y2=4的切线与x轴正半轴，y轴正半轴围成一个三角形，当该三角形面积最小时，切点为P（如图）．