题目内容
设a=ln2,b=(ln2)2,c=ln
,则( )
| 2 |
| A、a>b>c |
| B、a>c>b |
| C、c>a>b |
| D、c>b>a |
考点:对数值大小的比较
专题:函数的性质及应用
分析:利用对数的运算性质、作差法即可得出.
解答:
解:∵0<a=ln2<1,
∴b=(ln2)2,<ln2,
b-c=(ln2)2-ln
=ln2(ln2-
)=ln2(ln
-ln
)>0,
∴a>b>c.
故选:A.
∴b=(ln2)2,<ln2,
b-c=(ln2)2-ln
| 2 |
| 1 |
| 2 |
| 4 |
| e |
∴a>b>c.
故选:A.
点评:本题考查了对数的运算性质、作差法、不等式的性质,属于基础题.

练习册系列答案
相关题目
已知集合A={-1,0,1,2},B={x|1≤2x<4},则A∩B=( )
| A、{-1,0,1} |
| B、{0,1,2} |
| C、{0,1} |
| D、{1,2] |
已知tanα=4,tan(α-β)=-3,则tanβ=( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
下列函数中,在区间(0,1]上为增函数的是( )
| A、y=2x2-x+3 | ||
B、y=(
| ||
| C、y=x3 | ||
D、y=log
|
已知x,y满足不等式组
,则Z=x+2y的最小值为( )
|
| A、2 | B、3 | C、4 | D、-6 |
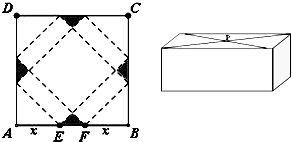
 在底面边长为2,高为1的正四梭柱ABCD-A1B1C1D1中,E,F分别为BC,C1D1的中点.则异面直线A1E,CF所成的角为
在底面边长为2,高为1的正四梭柱ABCD-A1B1C1D1中,E,F分别为BC,C1D1的中点.则异面直线A1E,CF所成的角为