题目内容
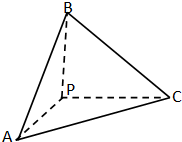 三棱锥P-ABC中,三侧棱PA,PB,PC两两互相垂直,且三角形△PAB,△PAC,△PBC的面积依次为1,1,2,则此三棱锥 P-ABC外接球的表面积为( )
三棱锥P-ABC中,三侧棱PA,PB,PC两两互相垂直,且三角形△PAB,△PAC,△PBC的面积依次为1,1,2,则此三棱锥 P-ABC外接球的表面积为( )| A、9π | B、12π |
| C、18π | D、36π |
考点:棱柱、棱锥、棱台的体积
专题:球
分析:通过已知条件可以求出PA,PB,PC的长度,并且以PA,PB,PC为过同一顶点的三条边作一个长方体,而这个长方体的外接球就是三棱锥P-ABC的外接球.根据PA,PB,PC的长可求出长方体的对角线长,而长方体的对角线就是外接球的直径,这样就可利用球的表面积公式求出该外接球的表面积.
解答:
解:由已知条件得:PA=1,PB=PC=2;
以PA、PB、PC为过同一顶点的三条棱,作长方体如图:

则长方体的外接球同时也是三棱锥P-ABC外接球;
∵长方体的对角线长为:
=3;
∴外接球的半径r=
;
∴三棱锥 P-ABC外接球的表面积为4πr2=9π.
故选A.
以PA、PB、PC为过同一顶点的三条棱,作长方体如图:

则长方体的外接球同时也是三棱锥P-ABC外接球;
∵长方体的对角线长为:
| PA2+PB2+PC2 |
∴外接球的半径r=
| 3 |
| 2 |
∴三棱锥 P-ABC外接球的表面积为4πr2=9π.
故选A.
点评:考查外接球的概念,而根据已知的三棱锥的三条侧棱两两垂直想到作一个长方体是求解本题的关键,以及长方体的体对角线就是该长方体外接球的直径,球的表面积公式.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知集合A={-1,0,1,2},B={x|1≤2x<4},则A∩B=( )
| A、{-1,0,1} |
| B、{0,1,2} |
| C、{0,1} |
| D、{1,2] |
若tanα=3,则sin2α+sin2α的值等于( )
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|

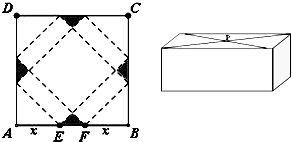
 在底面边长为2,高为1的正四梭柱ABCD-A1B1C1D1中,E,F分别为BC,C1D1的中点.则异面直线A1E,CF所成的角为
在底面边长为2,高为1的正四梭柱ABCD-A1B1C1D1中,E,F分别为BC,C1D1的中点.则异面直线A1E,CF所成的角为