题目内容
16.已知平行六面体ABCD-A′B′C′D′.求证:$\overrightarrow{AC}$+$\overrightarrow{AB}$+$\overrightarrow{AD}$=2$\overrightarrow{AC}$.分析 根据题意,画出图形,结合图形,利用向量的合成法则,即可证出结论.
解答 证明:如图所示,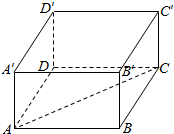
平行六面体ABCD-A′B′C′D′中,
$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{AC}$,
∴$\overrightarrow{AC}$+$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{AC}$+$\overrightarrow{AC}$=2$\overrightarrow{AC}$.
点评 本题考查了空间向量的线性表示与运算问题,是基础题目.

练习册系列答案
相关题目
7.在空间直角坐标系中,A(0,0,2),B(2,2,2),在平面xoy中找一点P,使得|PA|+|PB|最小,则点P的坐标为( )
| A. | (0,0,0) | B. | (2,2,0) | C. | (1,1,0) | D. | (0,1,0) |
4.已知是等差数列{an},且a2+a8=16,则数列{an}的前9项和等于( )
| A. | 36 | B. | 72 | C. | 144 | D. | 288 |
8.若f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x}-a.x≥\frac{1}{2}}\\{x+2-a,x<\frac{1}{2}}\end{array}\right.$的三个零点为x1,x2,x3,则x1x2x3的取值范围是( )
| A. | (0,+∞) | B. | (0,$\frac{3}{2}$) | C. | (0,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,$\frac{3}{2}$) |
5.已知sin(π+a)=$\frac{1}{2}$,则sin(9π+a)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
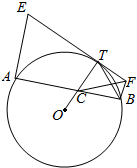 已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证:
已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证: