题目内容
11.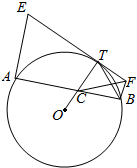 已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证:
已知AB是圆O的一条弦,过点A、B分别作AE⊥AB,BF⊥AB,交弧AB上任意一点T的切线于点E、F,OT交AB于点C,求证:(Ⅰ)∠CBT=∠CFT;
(Ⅱ)CT2=AE•BF.
分析 (Ⅰ)证明B,C,T,F四点共圆,可得∠CBT=∠CFT;
(Ⅱ)延长EF与ABM交于P,利用△PBF∽△PTC,△PAE∽△PTC,结合切割线定理,即可证明CT2=AE•BF.
解答  证明:(Ⅰ)∵OT⊥EF,BF⊥AB,∠CTF=∠CBF=90°,
证明:(Ⅰ)∵OT⊥EF,BF⊥AB,∠CTF=∠CBF=90°,
∴∠CTF+∠CBF=180°,
∴B,C,T,F四点共圆,
∴∠CBT=∠CFT;
(Ⅱ)延长EF与ABM交于P,则△PBF∽△PTC,
∴$\frac{PB}{PT}$=$\frac{BF}{CT}$①,
△PAE∽△PTC,∴$\frac{PA}{PT}$=$\frac{AE}{CT}$②
①×②$\frac{PA•PB}{P{T}^{2}}$=$\frac{AE•BF}{C{T}^{2}}$
由切割线定理可得PT2=PA•PB,
∴CT2=AE•BF.
点评 本题考查切割线定理的运用,考查三角形相似的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
1.已知向量$\overrightarrow a,\overrightarrow b$,其中$|\overrightarrow a|=1,|\overrightarrow b|=2$,且$\overrightarrow a⊥(\overrightarrow a-\overrightarrow b)$,则向量$\overrightarrow a$和$\overrightarrow b$的夹角是( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
6.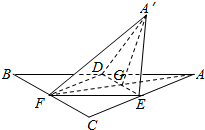 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 动点A′在平面ABC上的射影在线段AF上 | |
| B. | 恒有DE⊥平面A′GF | |
| C. | 三棱锥A′-FED的体积有最大值 | |
| D. | 异面直线A′E与BD不可能垂直 |