题目内容
8．若f（x）=$\left\{\begin{array}{l}{x+\frac{1}{x}-a．x≥\frac{1}{2}}\\{x+2-a，x＜\frac{1}{2}}\end{array}\right.$的三个零点为x1，x2，x3，则x1x2x3的取值范围是（ ）| A． | （0，+∞） | B． | （0，$\frac{3}{2}$） | C． | （0，$\frac{1}{2}$） | D． | （$\frac{1}{2}$，$\frac{3}{2}$） |
分析 令f（x）=0，由题意可得直线y=a和函数y=g（x）=$\left\{\begin{array}{l}{x+\frac{1}{x}，x≥\frac{1}{2}}\\{x+2，x＜\frac{1}{2}}\end{array}\right.$的图象有三个交点，画出它们的图象，求得x1，x2，x3的范围，结合函数式可得x2x3=1，即可得到所求范围．
解答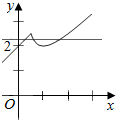 
解：令f（x）=0，可得直线y=a和函数y=g（x）=$\left\{\begin{array}{l}{x+\frac{1}{x}，x≥\frac{1}{2}}\\{x+2，x＜\frac{1}{2}}\end{array}\right.$的图象有三个交点，
分别作出直线y=a和函数y=g（x）的图象，
由图象可设0＜x1＜$\frac{1}{2}$，$\frac{1}{2}$＜x2＜1，1＜x3＜2，
由a=x1+2=x2+$\frac{1}{{x}_{2}}$=x3+$\frac{1}{{x}_{3}}$，可得x2-x3=$\frac{{x}_{2}-{x}_{3}}{{x}_{2}{x}_{3}}$，
即有x2x3=1，则x1x2x3=x1∈（0，$\frac{1}{2}$）．
故选：C．
点评 本题考查函数的零点的问题的解法，注意运用数形结合的思想方法，考查运算能力，属于中档题．
练习册系列答案
相关题目