题目内容
△ABC中，已知2A=B+C，且a2=bc，则△ABC的形状是（ ）
| A、两直角边不等的直角三角形 |
| B、顶角不等于90°，或60°的等腰三角形 |
| C、等边三角形 |
| D、等腰直角三角形 |
考点：正弦定理
专题：解三角形
分析：2A=B+C，A+B+C=π，可得A=
，由余弦定理可得：a2=b2+c2-2bccos
，又a2=bc，可得b=c，即可得出．
| π |
| 3 |
| π |
| 3 |
解答：
解：∵2A=B+C，A+B+C=π，
∴A=
，
由余弦定理可得：a2=b2+c2-2bccos
=b2+c2-bc，
∵a2=bc，
∴（b-c）2=0，
解得b=c．
∴△ABC是等边三角形．
故选：C．
∴A=
| π |
| 3 |
由余弦定理可得：a2=b2+c2-2bccos
| π |
| 3 |
∵a2=bc，
∴（b-c）2=0，
解得b=c．
∴△ABC是等边三角形．
故选：C．
点评：本题考查了余弦定理、三角形的内角和定理、等边三角形的判定定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
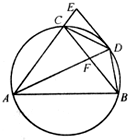如图，圆周角∠BAC的平分线与圆交于点D，过点D的切线与弦AC的延长线交于点 E，AD交BC于点F．
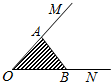如图，A，B分别是射线OM，ON上的两点，给出下列向量：①