题目内容
已知函数f(x)=ex-ax(a∈R,e为自然对数的底数)
(1)讨论函数f(x)的单调性;
(2)若a=1,函数g(x)=(x-m)f(x)-ex+x2+x在x∈(2,+∞)上为增函数,求实数m的取值范围.
(1)讨论函数f(x)的单调性;
(2)若a=1,函数g(x)=(x-m)f(x)-ex+x2+x在x∈(2,+∞)上为增函数,求实数m的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)求出函数f(x)的定义域,函数的导数(x)=ex-a
通过当a≤0时,当a>0时,分别判断函数的单调性.
(Ⅱ)当a=1时,化简g(x)=(x-m)(ex-x)-ex+x2+x,通过g(x)在x∈(0,+∞)上为增函数,转化g'(x)=xex-mex+m+1≥0在x∈(2,+∞)恒成立,推出m≤
在x∈(2,+∞)恒成立,通过构造新函数利用导数求出函数的最值,推出结果即可.
通过当a≤0时,当a>0时,分别判断函数的单调性.
(Ⅱ)当a=1时,化简g(x)=(x-m)(ex-x)-ex+x2+x,通过g(x)在x∈(0,+∞)上为增函数,转化g'(x)=xex-mex+m+1≥0在x∈(2,+∞)恒成立,推出m≤
| xex+1 |
| ex-1 |
解答:
解:(Ⅰ)函数f(x)的定义域为x∈R,f'(x)=ex-a
当a≤0时,f'(x)>0,所以f(x)在R上为增函数;
当a>0时,由f'(x)=0得x=lna
则:当x∈(-∞,lna)时,f'(x)<0,所以函数f(x)在(-∞,lna)上为减函数,
当x∈(lna,+∞)时,f'(x)>0,
所以函数f(x)在(lna,+∞)上为增函数.…(6分)
(Ⅱ)当a=1时,g(x)=(x-m)(ex-x)-ex+x2+x,
∵g(x)在x∈(0,+∞)上为增函数,∴g'(x)=xex-mex+m+1≥0在x∈(2,+∞)恒成立,
即m≤
在x∈(2,+∞)恒成立,
令h(x)=
,x∈(2,+∞),h′(x)=
=
,
令L(x)=ex-x-2,L'(x)=ex-1>0在x∈(2,+∞)恒成立,
即L(x)=ex-x-2在x∈(2,+∞)单调递增,
即L(x)>L(2)=e2-4>0,∴h'(x)>0
即h(x)=
在x∈(2,+∞)单调递增,h(x)>h(2)=
所以m≤
. …(12分)
当a≤0时,f'(x)>0,所以f(x)在R上为增函数;
当a>0时,由f'(x)=0得x=lna
则:当x∈(-∞,lna)时,f'(x)<0,所以函数f(x)在(-∞,lna)上为减函数,
当x∈(lna,+∞)时,f'(x)>0,
所以函数f(x)在(lna,+∞)上为增函数.…(6分)
(Ⅱ)当a=1时,g(x)=(x-m)(ex-x)-ex+x2+x,
∵g(x)在x∈(0,+∞)上为增函数,∴g'(x)=xex-mex+m+1≥0在x∈(2,+∞)恒成立,
即m≤
| xex+1 |
| ex-1 |
令h(x)=
| xex+1 |
| ex-1 |
| (ex)2-xex-2ex |
| (ex-1)2 |
| ex(ex-x-2) |
| (ex-1)2 |
令L(x)=ex-x-2,L'(x)=ex-1>0在x∈(2,+∞)恒成立,
即L(x)=ex-x-2在x∈(2,+∞)单调递增,
即L(x)>L(2)=e2-4>0,∴h'(x)>0
即h(x)=
| xex+1 |
| ex-1 |
| 2e2+1 |
| e2-1 |
所以m≤
| 2e2+1 |
| e2-1 |
点评:本题考查函数的导数的应用,函数的最值,构造法的应用,考查分析问题解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
△ABC中,已知2A=B+C,且a2=bc,则△ABC的形状是( )
| A、两直角边不等的直角三角形 |
| B、顶角不等于90°,或60°的等腰三角形 |
| C、等边三角形 |
| D、等腰直角三角形 |
如图所示的程序框图输出的结果是S=14,则判断框内应填的条件是( )


| A、i≥7? | B、i>15? |
| C、i≥15? | D、i>31? |
若集合A={x||x|<1},B={x|x2-2x<0},则A∩B=( )
| A、(-1,2) |
| B、(0,1) |
| C、(0,2) |
| D、(1,2) |
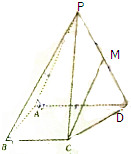 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,AD∥BC,∠ABC=90°,M是PD的中点,且AD=2AB=2BC=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,AD∥BC,∠ABC=90°,M是PD的中点,且AD=2AB=2BC=2.