题目内容
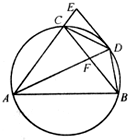 如图,圆周角∠BAC的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点 E,AD交BC于点F.
如图,圆周角∠BAC的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点 E,AD交BC于点F.(Ⅰ)求证:BC∥DE;
(Ⅱ)若D,E,C,F四点共圆,且
 |
| AC |
 |
| BC |
考点:与圆有关的比例线段
专题:推理和证明
分析:(Ⅰ)通过证明∠EDC=∠DCB,然后推出BC∥DE.
(Ⅱ)解:证明∠CFA=∠CED,然后说明∠CFA=∠ACF.设∠DAC=∠DAB=x,在等腰△ACF中,π=∠CFA+∠ACF+∠CAF=7x,求解即可.
(Ⅱ)解:证明∠CFA=∠CED,然后说明∠CFA=∠ACF.设∠DAC=∠DAB=x,在等腰△ACF中,π=∠CFA+∠ACF+∠CAF=7x,求解即可.
解答:
 解:(Ⅰ)证明:因为∠EDC=∠DAC,∠DAC=∠DAB,∠DAB=∠DCB,
解:(Ⅰ)证明:因为∠EDC=∠DAC,∠DAC=∠DAB,∠DAB=∠DCB,
所以∠EDC=∠DCB,
所以BC∥DE.…(4分)
(Ⅱ)解:因为D,E,C,F四点共圆,所以∠CFA=∠CED
由(Ⅰ)知∠ACF=∠CED,所以∠CFA=∠ACF.
设∠DAC=∠DAB=x,
因为
=
,所以∠CBA=∠BAC=2x,
所以∠CFA=∠FBA+∠FAB=3x,
在等腰△ACF中,π=∠CFA+∠ACF+∠CAF=7x,则x=
,
所以∠BAC=2x=
.…(10分)
 解:(Ⅰ)证明:因为∠EDC=∠DAC,∠DAC=∠DAB,∠DAB=∠DCB,
解:(Ⅰ)证明:因为∠EDC=∠DAC,∠DAC=∠DAB,∠DAB=∠DCB,所以∠EDC=∠DCB,
所以BC∥DE.…(4分)
(Ⅱ)解:因为D,E,C,F四点共圆,所以∠CFA=∠CED
由(Ⅰ)知∠ACF=∠CED,所以∠CFA=∠ACF.
设∠DAC=∠DAB=x,
因为
 |
| AC |
 |
| BC |
所以∠CFA=∠FBA+∠FAB=3x,
在等腰△ACF中,π=∠CFA+∠ACF+∠CAF=7x,则x=
| π |
| 7 |
所以∠BAC=2x=
| 2π |
| 7 |
点评:本题考查内错角相等证明直线的平行,四点共圆条件的应用,考查推理与证明的基本方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在某校的一次英语听力测试中用以下茎叶图记录了甲、乙两组各5名学生的听力成绩(单位:分)已知甲组数据的众数为15,乙组数据的中位数为17,则x、y的值分别为( )
在某校的一次英语听力测试中用以下茎叶图记录了甲、乙两组各5名学生的听力成绩(单位:分)已知甲组数据的众数为15,乙组数据的中位数为17,则x、y的值分别为( )| A、2,5 | B、5,5 |
| C、5,7 | D、8,7 |
△ABC中,已知2A=B+C,且a2=bc,则△ABC的形状是( )
| A、两直角边不等的直角三角形 |
| B、顶角不等于90°,或60°的等腰三角形 |
| C、等边三角形 |
| D、等腰直角三角形 |
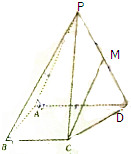 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,AD∥BC,∠ABC=90°,M是PD的中点,且AD=2AB=2BC=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是等边三角形,AD∥BC,∠ABC=90°,M是PD的中点,且AD=2AB=2BC=2.