题目内容
已知数列{an}满足a1=1,an+an-1=2n(n≥2),则数列{an}的前n项和Sn= .
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:确定奇数项、偶数项均以2为公差的等差数列,可得a2n-1=2n-1,a2n=2n+1,再分类讨论,即可得出结论.
解答:
解:∵数列{an}满足a1=1,an+an-1=2n(n≥2),
∴a2+a1=4,a3+a2=6,a4+a3=8,a5+a4=10,a6+a5=12,…,
∴a2=3,a3=3,a4=5,a5=5,a6=7
∴奇数项、偶数项均以2为公差的等差数列,
∴a2n-1=2n-1,a2n=2n+1,
n=2k时,Sn=
+
=2k2+2k=
;
n=2k-1时,Sn=S2k-a2k=2k2+2k-2k-1=2k2-1=
,
∴Sn=
.
故答案为:
.
∴a2+a1=4,a3+a2=6,a4+a3=8,a5+a4=10,a6+a5=12,…,
∴a2=3,a3=3,a4=5,a5=5,a6=7
∴奇数项、偶数项均以2为公差的等差数列,
∴a2n-1=2n-1,a2n=2n+1,
n=2k时,Sn=
| k(1+2k-1) |
| 2 |
| k(3+2k+1) |
| 2 |
| n(n+2) |
| 2 |
n=2k-1时,Sn=S2k-a2k=2k2+2k-2k-1=2k2-1=
| n2+2n-1 |
| 2 |
∴Sn=
|
故答案为:
|
点评:本题考查数列的通项与求和,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知直线y=(a-a2)x-2和y=(3a+1)x+1互相平行,则a的值等于( )
| A、2 | B、1 | C、0 | D、-1 |
某校高三年级学生会主席团有共有5名同学组成,其中有3名同学来自同一班级,另外两名同学来自另两个不同班级.现从中随机选出两名同学参加会议,则两名选出的同学来自不同班级的概率为( )
| A、0.35 | B、0.4 |
| C、0.6 | D、0.7 |
已知变量x,y满足约束条件
,则z=2x+y的最大值为( )
|
| A、2 | B、1 | C、-4 | D、4 |
函数y=ax-b(a>0且a≠1)的图象不经过第一象限,则( )
| A、a>1且b<-1 |
| B、a<1且b<-1 |
| C、a<1且b≥1 |
| D、a<1且b≤1 |
若实数x、y满足不等式组
则z=|x|+2y的最大值是( )
|
| A、10 | B、11 | C、13 | D、14 |
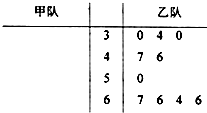 甲、乙两个竞赛队都参加了10场比赛,比赛得分情况记录如下(单位:分):
甲、乙两个竞赛队都参加了10场比赛,比赛得分情况记录如下(单位:分):