题目内容
在△ABC中,记∠BAC=x(角的单位是弧度制),△ABC的面积为S,且
•
=8,4≤S≤4
.求函数f(x)=2
sin2(x+
)+2cos2x-
的最大值、最小值.
| AB |
| AC |
| 3 |
| 3 |
| π |
| 4 |
| 3 |
考点:三角函数的最值,两角和与差的正弦函数,二倍角的正弦,二倍角的余弦
专题:解三角形,平面向量及应用
分析:由∠BAC=x,
•
=8,利用平面向量的数量积运算求得bccosx=8,结合正弦定理求面积得到S=4tanx,再由三角形面积的范围求得1≤tanx≤
,进一步得到x的取值范围.然后化简f(x),由x的范围求得f(x)的最值.
| AC |
| AB |
| 3 |
解答:
解:∵∠BAC=x,
•
=8,
∴bccosx=8,
又S=
bcsinx,∴S=4tanx,
∵4≤S≤4
,
∴1≤tanx≤
,而x为三角形一内角,
∴所求的x的取值范围是
≤x≤
.
f(x)=2
sin2(x+
)+2cos2x-
=
sin2x+cos2x+1=2sin(2x+
)+1,
∵
≤x≤
,
∴
≤2x+
≤
,
≤sin(2x+
)≤
.
∴f(x)min=f(
)=2,f(x)max=f(
)=
+1.
| AC |
| AB |
∴bccosx=8,
又S=
| 1 |
| 2 |
∵4≤S≤4
| 3 |
∴1≤tanx≤
| 3 |
∴所求的x的取值范围是
| π |
| 4 |
| π |
| 3 |
f(x)=2
| 3 |
| π |
| 4 |
| 3 |
=
| 3 |
| π |
| 6 |
∵
| π |
| 4 |
| π |
| 3 |
∴
| 2π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
∴f(x)min=f(
| π |
| 3 |
| π |
| 4 |
| 3 |
点评:本题考查了平面向量在解三角形中点应用,考查了三角函数的化简与求值,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知两条不同的直线a,b和平面α,那么下列命题中的真命题是( )
| A、若a⊥b,b⊥α,则a∥α |
| B、若a∥α,b∥α,则a∥b |
| C、若a⊥α,b⊥α,则a∥b |
| D、若a∥b,b∥α,则a∥α |
已知变量x,y满足约束条件
,则z=2x+y的最大值为( )
|
| A、2 | B、1 | C、-4 | D、4 |
函数y=ax-b(a>0且a≠1)的图象不经过第一象限,则( )
| A、a>1且b<-1 |
| B、a<1且b<-1 |
| C、a<1且b≥1 |
| D、a<1且b≤1 |
若实数x、y满足不等式组
则z=|x|+2y的最大值是( )
|
| A、10 | B、11 | C、13 | D、14 |
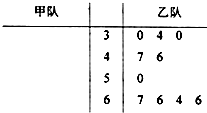 甲、乙两个竞赛队都参加了10场比赛,比赛得分情况记录如下(单位:分):
甲、乙两个竞赛队都参加了10场比赛,比赛得分情况记录如下(单位:分): 已知函数f(x)=sin(ωx-
已知函数f(x)=sin(ωx-