题目内容
9.中国古代数学名著《张丘建算经》中记载:“今有马行转迟,次日减半,疾七日,行七百里.”意思是:现有一匹马行走的速度逐渐减慢,每天走的里程数是前一天的一半,连续行走7日,共走了700里.若该匹马连续按此规律行走,则它在第8天到第14天这7天时间所走的总里程为( )| A. | 350里 | B. | 1050里 | C. | $\frac{175}{32}$里 | D. | .$\frac{22575}{32}$里 |
分析 设该匹马第一日走a1里,利用等比数列前n项和公式求出a1,由此利用等比数列前n项和公式能求出该匹马连续按此规律行走,则它在第8天到第14天这7天时间所走的总里程.
解答 解:设该匹马第一日走a1里,
∵马行走的速度逐渐减慢,每天走的里程数是前一天的一半,连续行走7日,共走了700里,
∴$\frac{{a}_{1}(1-\frac{1}{{2}^{7}})}{1-\frac{1}{2}}$=700,解得a1=350×$\frac{128}{127}$,
∴该匹马连续按此规律行走,则它在第8天到第14天这7天时间所走的总里程为:
S14-700=$\frac{350×\frac{128}{127}(1-\frac{1}{{2}^{14}})}{1-\frac{1}{2}}$-700=$\frac{175}{32}$(里).
故选:C.
点评 本题考查等比数列的第8项至第14项的和的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
19.某三棱锥的三视图如图所示,该三棱锥的体积是( )


| A. | 2 | B. | 4 | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
4.长方体ABCD-A1B1C1D1中,$DC+C{C_1}=8,CB=4,\overrightarrow{AM}=\overrightarrow{MB}$,点N是平面A1B1C1D1上的点,且满足${C_1}N=\sqrt{5}$,当长方体ABCD-A1B1C1D1的体积最大时,线段MN的最小值是( )
| A. | $6\sqrt{2}$ | B. | 8 | C. | $\sqrt{21}$ | D. | $4\sqrt{3}$ |
1. 如图,网格纸上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体外接球的表面积为
如图,网格纸上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体外接球的表面积为
( )
 如图,网格纸上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体外接球的表面积为
如图,网格纸上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体外接球的表面积为( )
| A. | 9π | B. | 18π | C. | 36π | D. | 144π |
18. 某几何体的三视图如图所示,则它的体积是( )
某几何体的三视图如图所示,则它的体积是( )
 某几何体的三视图如图所示,则它的体积是( )
某几何体的三视图如图所示,则它的体积是( )| A. | 8-2π | B. | 4-$\frac{2π}{3}$ | C. | 8-$\frac{2π}{3}$ | D. | 4-$\frac{π}{3}$ |
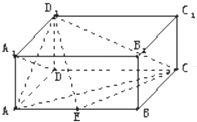 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AD上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AD上移动.