题目内容
1．
如图，网格纸上的小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体外接球的表面积为（ ）
| A． | 9π | B． | 18π | C． | 36π | D． | 144π |
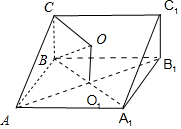
分析 由三视图可知：该几何体为一个横放的直三棱柱，高为4，底面是一个直角边长分别为2，4的直角三角形，其中下面的一个侧面为边长为4的正方形，对角线相交于点O1．则球心O满足OO1⊥侧面ABB1A1．设OO1=x，则x2+$（2\sqrt{2}）^{2}$=（2-x）2+$（2\sqrt{2}）^{2}$，解得x．可得该多面体外接球的半径r．
解答 解：由三视图可知：该几何体为一个横放的直三棱柱，高为4，底面是一个直角边长分别为2，4的直角三角形，其中下面的一个侧面为边长为4的正方形，对角线相交于点O1．
则球心O满足OO1⊥侧面ABB1A1．
设OO1=x，则x2+$（2\sqrt{2}）^{2}$=（2-x）2+$（2\sqrt{2}）^{2}$，解得x=1．
∴
该多面体外接球的半径r=$\sqrt{{1}^{2}+（2\sqrt{2}）^{2}}$=3．
表面积为4π×32=36π．
故选：C．
点评 本题考查了直三棱柱的三视图、勾股定理、空间线面位置关系、球的表面积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
12．已知正方体的外接球的体积是$\frac{32}{3}$π，则这个正方体的体积是（ ）
| A． | $\frac{64}{27}$ | B． | $\frac{{64\sqrt{3}}}{9}$ | C． | $\frac{64}{9}$ | D． | $\frac{{64\sqrt{3}}}{27}$ |
9．中国古代数学名著《张丘建算经》中记载：“今有马行转迟，次日减半，疾七日，行七百里．”意思是：现有一匹马行走的速度逐渐减慢，每天走的里程数是前一天的一半，连续行走7日，共走了700里．若该匹马连续按此规律行走，则它在第8天到第14天这7天时间所走的总里程为（ ）
| A． | 350里 | B． | 1050里 | C． | $\frac{175}{32}$里 | D． | .$\frac{22575}{32}$里 |
16．在平面几何中，可以得出正确结论：“正三角形的内切圆半径等于这个正三角形的高的$\frac{1}{3}$．”拓展到空间中，类比平面几何的上述结论，则正四面体的内切球半径等于这个正四面体的高的（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{8}$ |
