题目内容
17．已知5件产品中有2件次品，其余为合格品．现从这5件产品中任取2件，恰有一件次品的概率为$\frac{3}{5}$．分析 先求出基本事件总数，再求出恰有一件次品包含的基本事件个数，由此能求出恰有一件次品的概率．
解答 解：5件产品中有2件次品，其余为合格品．现从这5件产品中任取2件，
基本事件总数n=${C}_{5}^{2}$=10，
恰有一件次品包含的基本事件个数m=${C}_{3}^{1}{C}_{2}^{1}=6$，
∴恰有一件次品的概率p=$\frac{m}{n}$=$\frac{6}{10}$=$\frac{3}{5}$．
故答案为：$\frac{3}{5}$．
点评 本题考概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
7．若复数z满足$\frac{z+i}{-2{i}^{3}-z}$=i，则|$\overline{z}$+1|=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | 1 |
8．下列说法正确的是（ ）
| A． | |r|≤1；r越大，相关程度越大；反之，相关程度越小 | |
| B． | 线性回归方程对应的直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$至少经过其样本数据点（x1，y1），（x2，y2），（x3，y3），（xn，yn）中的一个点 | |
| C． | 在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高 | |
| D． | 在回归分析中，相关指数R2为0.98的模型比相关指数R2为0.80的模型拟合的效果差 |
5．直线y+2=k （x+1）恒过点（ ）
| A． | （2，1） | B． | （-2，-1） | C． | （-1，-2） | D． | （1，2） |
12．已知正方体的外接球的体积是$\frac{32}{3}$π，则这个正方体的体积是（ ）
| A． | $\frac{64}{27}$ | B． | $\frac{{64\sqrt{3}}}{9}$ | C． | $\frac{64}{9}$ | D． | $\frac{{64\sqrt{3}}}{27}$ |
2．
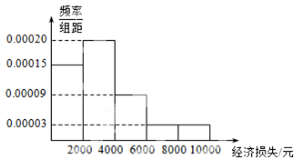适逢暑假，小王在某小区调查了50户居民由于洪灾造成的经济损失，将收集的数据分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五组，并作出频率分布直方图（如图）．
（Ⅰ）小王向班级同学发出为该小区居民捐款的倡议．若先从损失超过6000元的居民中随机抽出2户进行捐款援助，求这2户不在同一分组的概率；
（Ⅱ）洪灾过后小区居委会号召小区居民为洪灾重灾区捐款，小王调查的50户居民的捐款情况如表，在表格空白处填写正确的数字，并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？
参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=a+b+c+d为样本容量）．
适逢暑假，小王在某小区调查了50户居民由于洪灾造成的经济损失，将收集的数据分成[0，2000]，（2000，4000]，（4000，6000]，（6000，8000]，（8000，10000]五组，并作出频率分布直方图（如图）．（Ⅰ）小王向班级同学发出为该小区居民捐款的倡议．若先从损失超过6000元的居民中随机抽出2户进行捐款援助，求这2户不在同一分组的概率；
（Ⅱ）洪灾过后小区居委会号召小区居民为洪灾重灾区捐款，小王调查的50户居民的捐款情况如表，在表格空白处填写正确的数字，并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？
| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
9．中国古代数学名著《张丘建算经》中记载：“今有马行转迟，次日减半，疾七日，行七百里．”意思是：现有一匹马行走的速度逐渐减慢，每天走的里程数是前一天的一半，连续行走7日，共走了700里．若该匹马连续按此规律行走，则它在第8天到第14天这7天时间所走的总里程为（ ）
| A． | 350里 | B． | 1050里 | C． | $\frac{175}{32}$里 | D． | .$\frac{22575}{32}$里 |